La aventura de la ciencia: Pierre André Méchain

Detrás de infinidad de gestos cotidianos, como la medida del mueble del salón, del hueco de la escalera o del último estirón que ha dado la pequeña de la casa, puede haber grandes historias y aventuras que desconocemos, personas que han dedicado su esfuerzo y, en ocasiones su vida, la mayoría de las veces de forma anónima.Una de estas historias llevó a sufrir y morir en tierras españolas al más alto responsable de la astronomía francesa de principios del siglo XIX : Pierre André Méchain, director del Observatorio de París y presidente del Bureau des Longitudes .

El 19 de marzo de 1791 la Academia de las Ciencias de Paris aprobó, con el voto de Méchain, que el metro, la nueva medida que la Francia revolucionaria quería dar al mundo, sería la diezmillonésima parte del cuadrante de meridiano terrestre. La mayor empresa científica realizada hasta ese momento estaba en marcha, la medida de un arco de meridiano comprendido entre Dunkerque, al norte de Francia, y Barcelona iba a dar el valor de la nueva unidad con la mayor aproximación posible.

A comienzos de 1792 se emprenden los trabajos. El arco de meridiano que se debía medir se dividió en dos partes: el primero ( Dunkerke-Rodez), ya medido anteriormente, se volvería a medir y el tramo Rodez-Barcelona, el más difícil, quedaría a cargo de la persona más experimentada, Pierre André Méchain. La técnica a emplear sería la de la triangulación geodésica, se trazaría una cadena de triángulos, el vértice de los cuales serían montañas situadas a lo largo del meridiano.

Méchain decidió empezar por la parte española. Después de pedir el permiso y la colaboración correspondientes al rey de España Carlos IV, llegó a Barcelona en julio de 1792. Poco después los colaboradores españoles le sugieren que el arco acabe en Mallorca, en lugar de acabar en Barcelona, de esta forma, su mitad se situaría más exactamente sobre el paralelo 45 y comportaría ciertas ventajas matemáticas. En diciembre, su colaborador José González, capitán del bergantín Corzo, pasó a Mallorca para reconocer las montañas más convenientes y encender fuegos en las cimas para que Méchain comprobara si era posible la medida de un gran triángulo sobre el mar, operación nunca antes realizada ( los fuegos permitían hacer las mediciones de noche, cuando las neblinas superficiales disminuyen), pero, finalmente, los instrumentos de que disponían no lo permitieron, la óptica de los mismos no era suficientemente potente.

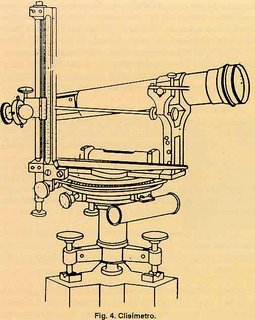
En enero de 1793, Luis XVI es guillotinado en Paris y poco después, en marzo, estalla la guerra entre España y Francia . A Méchain se le permite seguir con sus medidas que acaba en ese mismo año, pero no se le dejó volver a su país hasta 1794. Aquejado de fuertes depresiones tardó tres años más en hacer sus últimas medidas y, finalmente en agosto de 1798 se reune con Jean Baptiste Delambre, que había medido el resto del arco de meridiano, para revisar sus cálculos. El 22 de junio de 1799 se firmó el informe final por el primer cónsul Napoleón Bonaparte, había nacido la unidad de medida universal.


Sin embargo, la aventura del metro no había acabado, el 31 de agosto de 1802 el Bureau des Longitudes decide continuar con las operaciones geodésicas en España. Aunque finalmente es Méchain quien será el director del trabajo, muchos de sus colegas habrían preferido a alguien más joven. El 5 de mayo de 1803, Méchain vuelve a Barcelona, pero en esta ocasión su viaje iba a ser una pesadilla que acabó con su trágica muerte casi año y medio después.
Las reticencias que había desencadenado la reciente guerra, las trabas burocráticas en España, que retrasaron los medios materiales necesarios, y las contraórdenes del propio Bureau des Longitudes hicieron pasar al astrónomo por multitud de penalidades que no acabaron hasta que contrajo el paludismo por tierras valencianas . En la sierra Espadán se manifestaron los primeros síntomas, entonces escribe su última carta:” ... Esta desgraciada misión, el éxito de la cual está todavía tan lejano y resulta más que incierto, provocará muy probablemente mi perdición y, lo que es peor todavía, la de mi familia, mi tumba y la de mi honor...”.

Dos meses después, el 20 de septiembre de 1804, moriría entre los brazos de su amigo, Fausto Vallés y Vega, Barón de Pobla Tornesa. Una aventura que duró más de 13 años y costó la vida a su principal protagonista.


Nº43 Revista Mètode "La ciència i la Tragèdia, Pierre André Méchain (1744-1804), Antoni Ten. Universidad de Valencia.

Vacío cuantico, vacío fractal

El vacío estable y absoluto de Newton, con trayectorias continuas y determinadas, ha dejado paso al vacío cuántico asociado a unas extrañas trayectorias (*) discontinuas y fracturadas, llamadas por ello trayectorias fractales ( no son propiamente trayectorias). La existencia del cuanto de acción o constante de Planck ( se llama acción al producto de una energía por un tiempo ), base de la física cuántica, es la causa de ese cambio fundamental, y de otros muchos, con profundas consecuencias. Mediante la geometría fractal, este nuevo marco nos ofrece nuevas e interesantes perspectivas.


La existencia del cuanto de acción supone, realmente, la desaparición del vacío como tal. La mínima energía posible en el espacio (fluctuaciones cuánticas) deja de ser cero para pasar a depender del inverso de la distancia considerada. A la menor distancia posible (longitud de Planck = 10^-35 metros) , se le asocia una energía considerable, equivalente a una masa de 0,00002 gramos, y si mantuviéramos la misma relación, la masa correspondiente a un metro sería del orden de 1,2 x10²⁴ toneladas. Pero la propia existencia del mínimo cuanto de acción - principio de incertidumbre - determina que las fluctuaciones de energía del vacío queden acotadas, y sean cada vez menores conforme aumenta la distancia. Para las distancias macroscópicas, cotidianas para nosotros, son prácticamente nulas.

El vacío plano y estable ha dejado paso a un vacío cuántico modulado por sus fluctuaciones de energía que le dotan de una estructura fractal, discontinua. Dicha estructura, aparentemente extraña en la teoría, es por el contrario de lo más común en el mundo real. Cualquier superficie , por ejemplo, por lisa que nos parezca, al examinarla con un aumento progresivo la observaremos cada vez con mayores imperfecciones, hendiduras y discontinuidades. Ocurre con cualquier objeto del mundo real, la esfera, el cubo, o la línea perfecta no existen . No dejan de ser simplificaciones convenientes a las que asociamos conceptos sencillos y fáciles de manipular. Sin embargo las simplificaciones nos pueden ocultar detalles decisivos.

Supongamos que queremos recorrer, a pie, la distancia entre dos puntos determinados. Si la medimos sobre un plano, en línea recta, encontraremos una distancia determinada que se verá ampliamente superada cuando hagamos el trayecto en la realidad. Tendremos que subir, bajar, desviarnos un montón de veces de la trayectoria teórica preestablecida sobre el plano.En la realidad, habremos seguido una trayectoria fractal. Si ese mismo viaje lo hubiera hecho una hormiga, su trayectoria habría sido mucho más irregular que la nuestra y la distancia a recorrer mucho mayor , porque el paso de la hormiga es considerablemente menor que el humano.

Dimensión fractal = dimensión topológica + factor dimensional

( El factor dimensional, siempre positivo, es tanto mayor cuanto más irregular es el fractal)

En una línea perfecta eso no ocurre, pero en una trayectoria fractal si. Una línea teórica tiene dimensión topológica o aparente igual a la unidad, pero para una línea fractal existe un factor dimensional positivo , que se suma a la dimensión aparente para constituir la que llamamos dimensión fractal. Conforme sea más discontinuo e irregular un fractal mayor será este factor y , por tanto, mayor su dimensión fractal.


(En la figura ( representación del vacío cuántico), los trazos más anchos se corresponden con fermiones( quarks, electrones...) y sus antipartículas, mientras que los trazos más finos corresponden a bosones (gluones, fotones, W+, W-, Z0,...). En lo concerniente al color de los quarks y gluones, se corresponden con la carga de color de los mismos mientras que las partículas insensibles a la interacción fuerte aparecen en blanco o gris.)


(*) De hecho, no son propiamente trayectorias, las trayectorias clásicas no existen en mecánica cuántica .Concretamente, su dimensión fractal es 2 , pues por curioso que parezca existen fractales con dimensión entera.


(Reedición, ampliada, del post de fecha 06/06/2006 )

Premio Príncipe de Asturias de Investigación Científica

El físico español Juan Ignacio Cirac Sasturain, que dirige el departamento de óptica cuántica del Instituto Max Planck de Alemania(*), ha sido galardonado con el Premio Príncipe de Asturias de Investigación Científica. Nacido en 1965, se convierte en el ganador más joven en esta categoría.

Cirac Sasturain, natural de la localidad barcelonesa de Manresa, llegó a las últimas votaciones junto a las candidaturas conjuntas de los biólogos Ginés Morata y Peter Lawrence y de los químicos Avelino Corma y James Fraser Stoddar, a las que se impuso finalmente.

En el acta del jurado, presidido por el bioquímico Julio Rodríguez Villanueva, se le hace merecedor del premio "por su liderazgo mundial en la propuesta y desarrollo de la información cuántica, una nueva ciencia del siglo XXI que surge de combinar dos de las creaciones más notables de la ciencia del XX". Es decir, "de un lado la física cuántica, que explica el comportamiento de la materia a nivel atómico y subatómico, y del otro la teoría de la información, que describe el procesado, almacenamiento y transmisión de datos".

Añade que "el profesor Cirac es un referente internacional que ha producido algunas de las ideas más originales y brillantes tanto en el campo de la información cuántica como en el de la teoría cuántica de la luz y la física atómica". ( En la figura, qubits en nanotubo de carbono)

El jurado concluye señalando que "sus contribuciones están siendo decisivas para el desarrollo de comunicaciones completamente seguras, gracias a métodos de cifrado cuántico ( encriptación cuántica), y para la construcción de ordenadores potencialmente capaces de realizar en segundos cálculos que sobrepasan los límites actuales de la supercomputación" ( computación cuántica/ paralelismo cuántico) .

La computación mecanico-cuántica se basa en una propiedad misteriosa de la mecánica cuántica : la coherencia cuántica. En un ordenador actual la información se codifica en ceros (0) y unos (1). El estado de un bit ( unidad mínima de información) sólo puede encontrarse en (1) o en (0).

En un ordenador cuántico la unidad mínima de información es el qubit, un estado entrelazado, mezcla de los dos estados a la vez, de forma coherente. Para visualizarlo podemos imaginar una esfera, en el polo norte situariamos el (1) y en el polo sur el (0) : el qubit representaría cualquier punto de la esfera como una combinación de los dos estados a(0) + b(1). ( El (0) y el (1) constituirían lo que en música son los tonos puros musicales, en cambio, una superposición de (0) y (1) sería un acorde).

La potencia de la computación cuántica se basa en la coherencia que permite un efecto de paralelismo : Colocamos todos los qubits de entrada en idéntica superposición de ceros y unos, todos iguales. La computadora se encuentra entonces en otra superposición de todas las entradas posibles. Si hacemos pasar esta entrada a través de un circuito lógico que ejecute un determinado cómputo, el resultado es una superposición de todos los posibles resultados de ese cómputo: la computadora efectúa a la vez todos los cómputos posibles.

Símil musical: Una computadora cuántica que realice un cómputo ordinario, en el que no haya superposición de bits, genera una secuencia de ondas ( mecanico-cuánticas) análogas al sonido de un "cambio de repique" de los campanarios, en que las campanas se tañen una por vez. Un cómputo realizado en modo cuántico paralelo viene a ser como una sinfonía, su sonido corresponde a una multitud de ondas que se interfieren entre sí.

(*) La buena noticia es que tengamos científicos de esta talla, la mala noticia es que no trabajen en España. La endogamia de nuestra Universidad, seguro que no ayuda a solucionar el problema.
Fuentes: Agencia EFE y Revista Investigación y Ciencia TEMAS 10: "Misterios de la física cuántica" (4º trim.1997)

El efecto mariposa, un atractor extraño

El orden lleva asociado un grado importante de predicción, al caos le sucede lo contrario. Los sistemas lineales, representan el orden, son predecibles y cómodos de manejar, de ahí nuestra tendencia a generalizarlos. Ante un sinfín de situaciones generalizamos, proyectamos los datos del presente para tratar de averiguar un comportamiento futuro y casi siempre nos va bien. Pero existen sistemas que se resisten: pequeñas variaciones, incertidumbres, en los datos iniciales desembocan en situaciones finales totalmente descontroladas e impredecibles. Son los llamados sistemas caóticos ( En la figura, atractor extraño "poisson_saturne" hecho con el programa Chaoscope).


Para estudiar estos sistemas se requiere de una metodología diferente. Su estudio se realiza en el llamado espacio de fases, un espacio abstracto en el que se representan todas las variables dinámicas del sistema. Por ejemplo, un péndulo simple ideal se vería representado por dos variables, la velocidad y la posición de la masa suspendida. Su representación podría hacerse, por tanto, en el plano y sería una circunferencia. Cada punto de la misma representaría dos cantidades, la velocidad y la posición, en ese momento.


Esa figura en el espacio de fases, a la que se aproxima el fenómeno estudiado, se le llama su atractor. En los sistemas no caóticos el atractor suele ser un punto, una circunferencia, una figura geométrica conocida, pero en los sistemas caóticos presenta una forma “extraña”, de ahí que reciba el nombre de “atractor extraño”, con una dimensión fraccionaria o fractal ( En la figura, atractor de Lorenz, en 3D, con el programa Chaoscope).

El primero de éstos fue hallado, por casualidad, por el meteorólogo Edward Lorenz cuando trataba de encontrar un modelo matemático que permitiera predecir el comportamiento de grandes masas de aire. Consiguió ajustar el modelo a sólo tres variables que indican como cambian la velocidad y la temperatura del aire a lo largo del tiempo (atractor de Lorenz).


Después de haber estudiado el modelo, volvió a introducir los datos iniciales - esta vez con menos decimales- y el resultado que obtuvo fue completamente diferente del anterior. Cuando reflexionó sobre los resultados se dio cuenta que el sistema era extremadamente sensible a las condiciones iniciales: pequeñas perturbaciones en los datos de partida tienen una gran influencia sobre el resultado final. Sus ecuaciones captaban la esencia de la verdadera atmósfera. “Aquel primer día ( invierno de 1961) decidió que los pronósticos amplios estaban condenados a la extinción”. Pero vio más que azar en su modelo del tiempo: una fina estructura geométrica, orden disfrazado de casualidad.


Para explicar de una manera gráfica – y exagerada - la cuestión se le ocurrió que el simple aleteo de una mariposa, que no se hubiera tenido en cuenta en los datos iniciales, podía modificar una predicción hasta hacerla totalmente inviable después de un determinado tiempo.


Sobre el efecto mariposa se han escrito cientos de artículos, novelas, canciones y se han hecho películas. Recientemente he leído un artículo de Enrique Dans, profesor del Instituto de Empresa, en el que compara el “ecosistema de Internet” con los sistemas no lineales y complejos como el tiempo atmosférico:” Las variables en juego ( en Internet) no son tantas: si en el clima hablamos fundamentalmente de velocidad y temperatura del aire, en Internet hablamos de visitas, vínculos y cuestiones afines. Pero el posible impacto de una variación infinitesimal en medición de las variables de origen puede tener un impacto brutal en los resultados finales,...” . “ Criterios que todo el mundo, aparentemente, da por buenos, como el sacrosanto PageRank de Google, la cuenta de vínculos entrantes de una página web que lleva a cabo Technorati o los rankings de popularidad de Alexa son medidas completamente burdas, groseras, carentes de inteligencia, que responden únicamente al deseo e intentar reducir la incertidumbre, pero que lo hacen, en general, bastante mal.”


En este sentido nos encontramos en la era anterior al descubrimiento del efecto mariposa, utilizamos métodos lineales para tratar de analizar los sistemas complejos, no lineales, en donde las realimentaciones de todo tipo, y a todos los niveles, son la propia esencia del sistema. Necesitamos conocer "el atractor extraño de Internet".

Para saber más:"Caos,La creación de una ciencia", de James Gleik. Seix Barral. Barcelona 1988. Un magnífico libro

Los físicos y la metafísica

El post anterior acababa con unas reflexiones filosóficas del eminente físico Michio Kaku sobre el sentido de la vida. Aunque a algunos no les guste demasiado, los físicos son también personas y suelen pensar, más de lo que parece, en temas trascendentales. Esa aproximación a la persona fue la que me decidió a acabarlo así.

Por otra parte, en el libro de Michio Kaku, poco antes de esas reflexiones se citan unas palabras del propio Stephen Hawking ( cuando creía que la gran unificación de las interacciones fundamentales estaba próxima a llegar, al final del siglo XX ): “Si descubrimos una teoría completa, con el tiempo debería ser comprensible en sus principios generales para todo el mundo, no sólo para unos pocos científicos. Entonces todos nosotros, filósofos, científicos y simples personas normales, deberíamos ser capaces de tomar parte en la discusión acerca de la cuestión de por qué nosotros y el universo existimos. Si encontráramos la respuesta a ello, sería el triunfo final de la razón humana- pues entonces conoceríamos la mente de Dios.

Bien conocida es, también, la famosa frase atribuída a Einstein, sobre la mecánica cuántica: “ Dios no juega a los dados”. Otra frase suya relacionada con su apreciación de las claves que llevan al entendimiento de las leyes físicas decía: ”Dios es sutil, no malicioso” ( es impresionante). Finalmente, en otra de sus reflexiones decía:” Creo en el Dios de Spinoza que se manifiesta en la ordenada armonía de lo que existe, no en un Dios que se preocupa del destino y de las acciones del ser humano”.

Roger Penrose, uno de los físico-matemáticos más eruditos y creativos del mundo roza la metafísica al ocuparse exhaustivamente del problema filosófico de la conexión “mente-cuerpo”. En su famoso libro “La nueva mente del emperador”, recorre la teoría de la relatividad, la mecánica cuántica y la cosmología persiguiendo esta trascendente cuestión. Se revela como un filósofo de primera fila, que no teme abordar problemas que los filósofos contemporáneos despachan calificándolos de sin sentido.

El eminente físico David Bohm, tuvo una estrecha relación con el filósofo Krishnamurti que influyó de una manera decisiva en la formulación de su teoría física sobre el orden plegado-desplegado y el paradigma holográfico. Su interpretación “apóstata” de la mecánica cuántica.

En uno de los últimos post comentaba, también sobre este aspecto de Dirac: Para Dirac, Díos debía ser un gran matemático y con las matemáticas que conocemos nos acercamos a conocer un trocito de su creación. Curiosamente, Dirac era un gran ateo. Al respecto, Pauli escribió bromeando en sus memorias: "Si entiendo correctamente a Dirac, él dice: no hay Dios, y Dirac es su profeta".

Paul Davies, profesor de matemáticas aplicadas en el King`s College de Londres y catedrático de física teórica en la Universidad de newcastle, tiene todo un libro dedicado a "Dios y la nueva física".

Finalmente, creo que los físicos que han llegado a entender en profundidad la armonía y belleza que encierran las leyes naturales no pueden dejar de pensar en una cierta transcendencia, crean o no crean en Dios. Sienten que la grandeza de los misterios que tratan de sondear traspasan lo puramente físico.

Metafísica, título dado por el filósofo peripatético Andrónico de Rodas al conjunto de 14 libros del filósofo griego Aristóteles que, cuando fueron recopilados y editados por aquél (c. 70 a.C.), se encontraban “después de (la) física” (en griego, meta (ta) physica). Su contenido versa sobre lo que el propio Aristóteles definía como primera filosofía: el estudio del ser (aquello más general y común que comparten todas las entidades y cuyos rasgos son universales). Es una de las principales obras de la antigua filosofía griega y constituye una de las más influyentes de toda la historia de la filosofía occidental. Su título da nombre a una de las principales ramas filosóficas, la metafísica.

La función modular de Ramanujan y la teoría de cuerdas

La teoría de cuerdas supone que cada modo o vibración de una cuerda fundamental representa una partícula elemental distinta, y puede explicar a la vez la naturaleza de la materia y del espacio-tiempo (las partículas en lugar de ser puntuales pasan a ser unidimensionales). Es la primera teoría cuántica de la gravedad: Cuando se calcularon por primera vez las ligaduras de autoconsistencia que impone la cuerda sobre el espacio-tiempo, se observó con sorpresa que las ecuaciones de Einstein ( teoría de la gravedad) emergían de la cuerda, de hecho, el gravitón o cuanto de gravedad era la menor vibración de la cuerda cerrada.

No sabemos todavía por qué la teoría de cuerdas está definida sólo en 10 y 26 dimensiones, aunque parece seguro que esta teoría no podría unificar las fuerzas fundamentales con tan solo tres dimensiones. Las cuerdas se rompen y se forman en el espacio N-dimensional arrastrando con ellas una serie de términos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos aparecen multiplicados por el factor (N-10), lo que nos obliga a elegir N=10 para eliminarlos.

Los teóricos de cuerdas al intentar manipular los diagramas de lazos KSV ( Kikkawa-Sakita-Virasoro) creados por las cuerdas en interacción encuentran unas extrañas funciones llamadas modulares que aparecen en las ramas más distantes e “inconexas” de las matemáticas((Yutaka Taniyama ( Japón, 1927-1958) observó que cada función modular está relacionada con una curva elíptica. Esto forma la base de la conjetura Taniyama-Shimura que demostró ser una parte importante en la demostración del Último Teorema de Fermat de Andrew Wiles )). Una función que aparece continuamente en la teoría de funciones modulares se denomina función de Ramanujan, en honor al matemático Srinivasa Ramanujan, nacido en 1887 en Erode, India, cerca de Madrás.

Ramanujan, trabajando en total aislamiento ( y sin formación, toda su instrucción matemática la consiguió de la lectura de un oscuro y olvidado libro de matemáticas escrito por George Carr), fue capaz de redescubrir por sí mismo lo más valioso de cien años de matemáticas occidentales y de dejarnos una obra, que consta de 4.000 fórmulas en cuatrocientas páginas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario ni demostración. Tenía tal intuición que los teoremas simplemente fluían de su cerebro, sin el menor esfuerzo aparente. Solía decir que las diosas Namakkal le inspiraban la fórmulas en sueños.

Trabajaba en el puerto franco de Madrás, en un trabajo servil con una mísera paga, pero tenía la suficiente libertad y tiempo para seguir con sus sueños matemáticos. Después de enviar varias cartas a tres matemáticos británicos conocidos, consiguió que el brillante matemático de Cambridge Godfrey H. Hardy se diera cuenta de su inmenso genio matemático y lo trajo a Cambridge en 1914. Hardy tratando de estimar la capacidad matemática de Ramanujan, concedía un 80 al gran matemático David Hilbert, un 100 a Ramanujan y un 25 a sí mismo.


La función de Ramanujan contiene un término elevado a la potencia veinticuatro. Ese número es el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas, pues cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando se generaliza la función de Ramanujan,el número 24 queda reemplazado por el 8. Si tenemos en cuenta que se añaden dos dimensiones más al número total de vibraciones que aparecen en una teoría relativista, obtendremos 8+2, ó 10: La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer autoconsistente.

Pura geometría para explicarlo todo, el sueño de Einstein. Y las matemáticas más extrañas imaginadas por un genio, sin apenas instrucción básica, para introducirnos en una teoría de cuerdas que necesita de matemáticas que todavía desconocemos. Einstein tenía las matemáticas inventadas por Riemann para su teoría de la relatividad general, la teoría de cuerdas quizás necesite de las matemáticas, que descansan en los cuadernos llenos de teoremas sin demostrar, de Ramanujan. En el fondo, siempre, una hermosa conexión entre las ramas más distantes e inconexas de las matemáticas y la propia realidad que representan las leyes físicas.

Para saber mucho más: "HIPERESPACIO", de Michio Kaku,( 1996 CRÍTICA-Grijalbo Mondadori,S.A. Barcelona) profesor de física teórica en la City University de Nueva York. Es un especialista a nivel mundial en la física de las dimensiones superiores ( hiperespacio). Despide el libro con una palabras preciosas:”Algunas personas buscan un significado a la vida a través del beneficio personal, a través de las relaciones personales, o a través de experiencias propias. Sin embargo, creo que el estar bendecido con el intelecto para adivinar los últimos secretos de la naturaleza da significado suficiente a la vida”.

DIOS DIJO:"QUE NEWTON SEA"

Tengo sobre la mesa el viejo y manoseado libro que aparece en la figura. Lo abro por el capítulo III y leo:
“DIOS DIJO;”QUE NEWTON SEA (*)”... “ El año en que Galileo moría en su reclusión de Florencia, un niño prematuro, bautizado con el nombre de Isaac, nacía en la familia de un agricultor del Licolnshire apellidada Newton. Durante los primeros años de escuela Isaac no dio signos de su futura grandeza. Era un muchacho enfermizo, tímido, más bien retrasado en sus estudios. Lo que le sacó de este estado fue su primera riña con un compañero de la escuela que, además de ser uno de los mejores estudiantes de la clase, era muy agresivo hacia los otros muchachos. Al recibir un golpe en el vientre que le asestó este camorrista (cuyo nombre se ha perdido para la historia ), Newton le desafió a luchar y le venció a causa de su "espíritu superior y resolución". Después de haber ganado en el aspecto físico, decidió completar su victoria en la batalla de la inteligencia y, trabajando esforzadamente, llegó a ser el primero de su clase. Después de ganar otra batalla con su madre que quería dedicarle a la agricultura, entró en el Colegio de la Trinidad a la edad de 18 años y se consagró al estudio de las matemáticas. En el año 1665, Newton tomó su grado de bachiller en artes sin ninguna distinción especial."

Cuando yo tenía unos 15 años en mi primer viaje, con mis padres, a Madrid me lo compré y empecé a leerlo. Su lectura me atrapó como sólo pueden hacerlo los buenos libros a esas edades. Consiguió que imaginara la aventura de la ciencia como una aventura más, y a sus personajes como los protagonistas de los libros de piratas y aventuras.

George Gamow, en su prólogo ( Univ. De Colorado, 1 de junio de 1960) dice:” En el presente libro, he intentado seguir un camino intermedio ( entre los libros de texto y los históricos) exponiendo lo mismo el proceso de Galileo que las leyes fundamentales de la mecánica por él descubiertas o presentando mis recuerdos personales sobre Niels Bohr junto con una detallada discusión del modelo del átomo de este físico... espero que este libro servirá para que los jóvenes lectores ( y acaso algunos viejos) sientan el impulso de estudiar Física; esta es su finalidad principal.

El libro se divide en los siguientes capítulos:
I. La aurora de la Física.
II. Las edades oscuras y el Renacimiento.
III. Dios dijo:"Que Newton sea".
IV. El calor como energía.
V. La edad de la electricidad.
VI. La revolución relativista.
VII. La ley de los cuanta.
VIII. El núcleo atómico y las partículas elementales.

Este post pretende brindar a este libro y a su autor mi pequeño homenaje y el de mis posibles lectores. ( Después de esto me voy a comprar una edición moderna del libro y a retirar, a un merecido descanso, la edición super-antigua de la foto).

(*)De unos versos de Alexander Pope (1688-1744):"La Naturaleza y sus leyes yacían ocultas en la noche; Dios dijo:"Que Newton sea", y todo se hizo luz."

El efecto Microsiervos sobre La Bella Teoría.

Ayer sobre las 12 de la mañana observé una auténtica avalancha de visitas, como se observa en el grafico. Rápidamente, constaté que provenía de Microsiervos y al visualizar la página leí, entre emocionado y atónito, el increíble post que hacía referencia a mi blog:





Guardando las distancias, me sentí como el pequeño sapo besado por la princesa del cuento. Amigos de Microsiervos, Alvy, muchísimas gracias.

El condensado de Bose-Einstein, un superátomo.

En junio de 1995, en el Instituto JILA (Joint Institute for Laboratory Astrophysics) de, Boulder, Colorado se creó una minúscula gota formada por 2000 átomos de rubidio enfriados hasta una temperatura de 100 milmillonésimas de grado sobre el cero absoluto. Durante 10 segundos se consiguió que perdieran su identidad individual y se comportaran como si fuesen un solo “superátomo”. Sus ecuaciones de onda individuales, que describen su posición y velocidad, se fundieron en una sola y los átomos se volvieronn indistinguibles entre sí.

Este experimento del fenómeno que predijo Einstein hace más de 70 años, después de estudiar los trabajos sobre una estadística especial que desarrolló Satyendra N. Bose para fotones, les valió el Premio Nobel en el año 2001 a Eric A.Cornell, Wolfgang Ketterle y a Carl E. Weiman.

En la condensación de Bose-Einstein la naturaleza ondulatoria de cada átomo está en fase con la de los demás, hasta tal punto que las ondas mecanocuánticas atraviesan la muestra entera y se observan a simple vista. Todos los átomos ocupan – a la vez- el mismo volumen de espacio, se mueven a la misma velocidad y dispersan luz del mismo color. Abre un campo precioso para el estudio de las viejas paradojas de la mecánica cuántica, pues las propiedades de lo microscópico se proyectan en lo macroscópico para poderlas estudiar con todo lujo de detalles.

Unos años antes, en 1997, se reconoció con el Premio Nobel de Física a Steven Chu, Claude Cohen-Tannoudji y William D Phillips el trabajo desarrollado para enfriar y atrapar átomos con luz láser. Precisamente este es uno de los dos métodos utilizados, en el experimento: primero se agrupan los átomos, en el centro de un recipiente de cristal, mediante la incidencia de seis haces de luz láser. Se ajusta su frecuencia de tal manera que los átomos que viajan en sentido opuesto al haz de luz dispersen muchos más fotones que los del sentido opuesto, lo que origina que vayan perdiendo velocidad y por tanto se "enfríen". Se apagan los láseres, y a continuación se produce un campo magnético que actúa a modo de "cuenco" dejando que salgan los átomos más energéticos y confinando, todavía más, los restantes.

A 200 milmillonésimas de grado sobre el cero absoluto, podemos observar la figura de la izquierda, donde las funciones de onda de los átomos forman una ligera cresta, pues sus velocidades todavía se encuentran dispersas. Conforme bajamos la temperatura llegamos a la figura de la cresta pronunciada: en ese momento se ha producido el condensado. Los átomos del mismo han alcanzado el nivel más bajo de energía y comparten ese mismo nivel, tal como estipula la mecánica cuántica. Se observa, a simple vista, la imagen de la derecha: una especie de cereza formada por los átomos que rodean el condensado, con el núcleo central que es el condensado de Bose-Einstein ( Figura superior ).

Actualmente ya se consiguen condensados de mas de 20 millones de átomos. Si imaginamos un condensado con dos millones de átomos, haciendo incidir un láser suficientemente localizado, podremos dividirlo en dos mitades y separarlas por completo. Podríamos suponer que un millón de átomos están en un paquete y el resto en el otro, pero la física cuántica nos dice que cada uno de los dos millones de átomos está en los dos sitios a la vez, siempre que no intentemos medir su número en cada paquete. Si lo hacemos destruiremos la coherencia entre las dos partes de la onda atómica y tendremos que hablar de dos condensados completamente independientes.

Las posibilidades que ofrecen este tipo de condensados son extraordinarias. Ultimamente, como ejemplo, se habla de un experimento que podría comprobar algunas predicciones de la física de supercuerdas, la rama de la física que intenta unificar todas las fuerzas de la naturaleza.


( En la figura inferior: Científicos del Georgia Institute of Technology durante sus experimentos con condensados Bose-Einstein )