Agujeros de gusano:¿el viaje en el tiempo?(cont.)

El viaje en el tiempo ha despertado desde siempre un gran interés , se han escrito libros y se han hecho películas sobre el tema, pero sólo desde hace poco se ha empezado a tratar desde el rigor científico, de acuerdo con los últimos conocimientos – todavía en mantillas- sobre gravedad cuántica.


El primer artículo sobre el tema salió a la luz en el verano de 1988, en la revista Physical Review Letters, firmado por Kip S. Thorne y dos colaboradores suyos, Michael S. Morris y Ulvi Yurtsever.

Según el mismo Thorne, en su libro “Agujeros negros y tiempo curvo” ( presentación de Stephen Hawking), existen dos estrategias para construir un agujero de gusano, una que se podría llamar estrategia cuántica y la otra estrategia clásica.

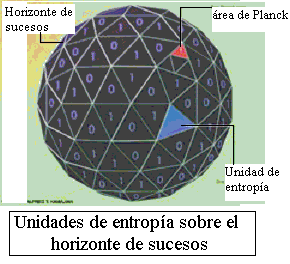
La estrategia cuántica se basa en las fluctuaciones gravitatorias cuánticas del vacío que ocurren en cualquier lugar del espacio-tiempo. En 1955, John Wheeler, combinando la mecánica cuántica con la relatividad general dedujo que en una región del tamaño de la longitud de Planck-Wheeler ( 1,62 x 10^–33 centímetros) las fluctuaciones del vacío son tan grandes que el espacio tal como lo conocemos hierve y se convierte en borbotones de espuma cuántica, el mismo tipo de espuma cuántica que constituye el corazón de una singularidad espacio-temporal como pueda ser un agujero negro.


A partir de esta espuma cuántica, con la tecnología adecuada podría detectarse un agujero de gusano y amplificarlo hasta un tamaño clásico. Sin embargo no comprendemos todavía lo bastante bien las leyes de la gravedad cuántica y ni siquiera la propia espuma cuántica probabilística.

La estrategia clásica pasa por tratar de deformar y retorcer el espacio a escalas macroscópicas para hacer un agujero de gusano, donde previamente no existía ninguno. Existe un método para construir un agujero de gusano mediante una deformación y retorcimiento suaves, sin producir singularidades ( sitios donde no funcionan las leyes físicas tal como las conocemos actualmente). En 1966 Robert Geroch, en Princeton, utilizó métodos topológicos para demostrarlo, pero sólo puede hacerse si durante la construcción el tiempo también se retuerce ( tiempo curvo) visto desde todos los sistemas de referencia. Concretamente, mientras se procede a la construcción debe ser posible viajar hacia atrás en el tiempo tanto como hacia adelante. La maquinaria que haga la construcción debe funcionar brevemente como una máquina del tiempo, desde los momentos finales a los momentos iniciales de la construcción.


Como decía en el post anterior, el legado de Eisntein llevado hasta el límite de sus posibilidades por físicos de la talla de Penrose, Wheeler, Thorne o Hawking, nos muestra una serie de fenómenos, como los agujeros de gusano, que parecen salidos de una novela de ciencia ficción. Sin embargo, para ser realistas, las leyes de la gravedad cuántica – lo que conocemos de ellas hasta ahora- nos están ocultando la respuesta definitiva a si los agujeros de gusano pueden convertirse con éxito en máquinas del tiempo. Se sospecha que el propio haz creciente de las fluctuaciones del vacío – multiplicado por efecto del propio agujero de gusano- puede ejercer una especie de protección cronológica que impida el viaje en el tiempo. Stephen Hawking, con su característico humor irónico describe esto como una conjetura que “ mantendría el mundo a salvo de la mirada directa de los historiadores”.

Agujeros de gusano, ¿el viaje en el tiempo?

El legado de Einstein ha llevado a científicos como Kip S. Thorne, Hawking, John Wheeler, Penrose y tantos otros a una gran búsqueda para descubrir dónde y cómo falla la relatividad y qué puede reemplazarla. Cuando tenemos una gran teoría hay que exprimirla al máximo, probarla hasta los mayores extremos, a veces por caminos extraños. En el caso de la relatividad están plagados de objetos tan exóticos como agujeros negros, enanas blancas, estrellas de neutrones, ondas gravitatorias, agujeros de gusano, distorsiones o máquinas del tiempo.

El sendero por el que discurre la ciencia está lleno de avances a trompicones, o de callejones sin salida y golpes de intuición, está muy lejos de ser una autopista con varios carriles, como a veces nos parece. Al final puede encontrarse la respuesta que se busca o constatar que la mayor parte del tiempo se ha perdido para nada.

Los agujeros de gusano:

Los llamados agujeros de gusano, una especie de pasadizo entre dos puntos distantes o no del espacio-tiempo, fueron descubiertos matemáticamente en 1916 por Ludwing Flamm, unos pocos meses después de que Einstein formulara su ecuación de campo ( relatividad general), como una solución a dicha ecuación de campo. Posteriormente, en los años cincuenta fueron investigados intensamente mediante gran variedad de cálculos matemáticos por John Wheeler y su equipo. Durante muchos años, los cálculos parecían indicar que se creaban en algún instante de tiempo y rápidamente se estrangulaban y se cerraban. Pero en 1985 , cuando Kip S. Thorne trataba de resolver un grave problema que tenía Carl Sagan con la heroína de su última novela , realizó una serie de cálculos que le llevaron a encontrar la solución a la inestabilidad de un presunto agujero de gusano.

La solución que encontró Thorne pasaba por un tipo de energía llamada exótica o energía negativa. A diferencia de la materia o energía normal o positiva que actúa, en grandes concentraciones como puede ser una estrella masiva, como una lente gravitatoria convergente ( hace converger los rayos de luz) la energía exótica o negativa actúa como lente gravitatoria divergente, manteniendo separadas las paredes del agujero de gusano. Hace divergir los rayos de luz que entren así como las fluctuaciones del vacío que de otra forma al ser multiplicados por el agujero impedirían su estabilidad y lo destrozarían.

El material exótico es más común de lo que nos podría parecer, de hecho las fluctuaciones del vacío que lo envuelven todo están formadas por energía positiva y energía negativa que en circunstancias normales producen una suma nula. Sin embargo Robert Wald ( colaborador de Wheeler) y Ulvi Yurtsever demostraron en los ochenta que en el espacio-tiempo curvo ( cerca de una gran masa), en una gran variedad de circunstancias, la curvatura distorsiona las fluctuaciones del vacío y las hace exóticas ( energía negativa).

Viaje en el tiempo:



Si mantenemos abierto un agujero de gusano mediante el aporte de energía negativa ( suponiendo que tenemos los medios técnicos necesarios que deberá tener una sociedad superavanzada en el futuro), podemos construir una máquina del tiempo. Una de las bocas del agujero podría permanecer en la Tierra y la otra boca la suponemos dentro de una nave interestelar. Si esta nave viaja a una velocidad cercana a la luz durante 24 horas ( tiempo de la nave, que pasa más lentamente por efecto relativista), el tiempo en la Tierra correspondiente podría ser de 15 años, por ejemplo. Cuando la nave regresa después de 24 horas de su tiempo, por la boca del agujero que ha permanecido en la nave podríamos volver al pasado, 15 años atrás. El agujero conectaría dos espacio-tiempos separados 15 años, su limitación de viaje al pasado la fijaría el instante en que se formó el agujero, antes no nos podríamos remontar porque no estaba abierto.


Según la teoría de la relatividad general, si se pueden mantener abiertos los agujeros de gusano mediante material exótico, el viaje en el tiempo viene condicionado por el mismo momento de la creación del agujero. No se puede viajar a un tiempo anterior a la propia creación del agujero de gusano.

Figuras: La primera es una descripción esquemática de un agujero de gusano. Comunica dos lugares espaciotemporales diferentes que podrían estar a años luz el uno del otro. La segunda es un agujero negro absorbiendo materia de una estrella compañera. La tercera es una máquina del tiempo con "tecnología" del siglo XIX.

¡¡¡Feliz Navidad , feliz año 2007 y felices fiestas en compañía de vuestra familia y amigos!!!

Dragones alados y agujeros negros (*)

Los agujeros negros, esas extrañas y poderosas criaturas intuidas por la relatividad general de Einstein, son a esta época y sociedad técnica como los terribles y alados dragones de fuego eran al medioevo. Posiblemente, gozan de las mismas características de seres extraordinarios mitad verdad, mitad mentira, de las que gozaban aquellos dragones míticos. Y sin embargo son reales.

Técnicamente responden a lo que se llama una singularidad del espacio-tiempo, es decir, son lugares en donde la materia, el espacio y el tiempo colapsan. En un agujero negro dejan de tener sentido las leyes físicas tal y como las conocemos. Es un objeto estelar en donde la materia está tan comprimida, es tan densa, como toda la masa de la Tierra apretujada en la cabeza de un alfiler. Por efecto de la atracción gravitatoria que se genera ni los propios rayos de luz son capaces de escapar. En consecuencia vemos una especie de agujero sin luz, al que llamamos “agujero negro”.

El agujero negro es el resultado del último estadio de la vida de ciertas estrellas. A partir de una cierta masa, cuando el combustible nuclear de la estrella se acaba, las reacciones termonucleares no pueden impedir que la fuerza de la gravedad atraiga toda la materia de la estrella hacia el centro de la misma.

En las proximidades del llamado horizonte de sucesos del agujero, el lugar donde la materia, tal como la conocemos, conoce el último estadio antes de ser engullida, la distorsión del espacio y del tiempo es de tal calibre que una nave espacial que se encontrara allí la veríamos como suspendida, quieta, en reposo mientras que los tripulantes de la misma estarían experimentando una caída a gran velocidad hacia el abismo negro. Su tiempo y el nuestro quedan disociados debido al desmesurado efecto de la gravedad en las proximidades del agujero. El espacio queda también terriblemente distorsionado por un efecto brutal de marea: a pequeñas distancias la fuerza de atracción es extremadamente variable, de modo que una barra de hierro se estiraría como un chicle. Allí prolifera la llamada materia exótica capaz de desencadenar una especie de minúsculos túneles en el espacio tiempo que son no menos interesantes que los agujeros negros. Esos túneles son llamados “agujeros de gusano” y son capaces, al menos en teoría, de comunicar dos lugares distantes en el espacio y en el tiempo. Su estabilidad y tamaño vienen determinados por la cantidad de materia exótica que les aportemos y son la respuesta hipotética a los viajes interestelares a galaxias que se encuentren a millones de años-luz de nosotros.

Agujeros negros, agujeros de gusano, túneles en el espacio-tiempo, viajes en el tiempo, distorsión espacial y temporal, todos estos conceptos que parecen sacados de una novela de ciencia ficción, forman parte ya de la ciencia seria que se investiga en la actualidad, y no deja de ser una paradoja que la física, la ciencia más pura y dura, se ocupe de cuestiones, en otro tiempo, esotéricas. La materia a la que nos agarramos como lo más sólido, simple y real que tenemos se está convirtiendo, cada vez más, en algo lleno de misterio y complejidad. La física cuántica y la teoría de la relatividad general nos la presentan como algo siempre en movimiento que se confunde con el propio espacio y tiempo. Conforme tratamos de entender sus propias entrañas se nos aparece como formando una especie de entidad compleja que algún premio Nóbel no ha dudado en llamar: la materia-espacio-tiempo. Las extrañas criaturas que dan nombre a este artículo han contribuido, con la curiosidad que han despertado entre loas físicos, a comprender mejor el mundo que nos rodea. En cierta forma su negra belleza ha arrojado un rayo de luz sobre nuestro conocimiento del universo que nos cobija.

Para saber más:
KIP S. THORNE (1995),”Agujeros negros y tiempo curvo”, ed. Crítica. Barcelona.
ROGER PENROSE(1991),”La nueva mente del emperador”, ed.Grijalbo Mondadori. Barcelona.
GILLES COHEN-TANNOUDJI Y MICHEL SPIRO(1988),”La materia-espacio-tiempo”, Espasa-Universidad.Madrid.
STEPHEN W. HAWKING Y ROGER PENROSE(1994),”Cuestiones cuánticas y cosmológicas”, Alianza Universidad.Madrid.
MICHIO KAKU(1996),”Hiperespacio”,ed.Crítica.Barcelona.

(*)Reedición del post del mismo nombre de 8/01/06.

El humor y la ciencia. Ciencia divertida

El humorismo, como decía el brillante Carlo M. Cipolla en su genial libro “Allegro ma non troppo”, es claramente la capacidad inteligente y sutil de poner de relieve y destacar el aspecto cómico de la realidad. No debe suponer una posición hostil, sino más bien una profunda y a menudo indulgente simpatía humana, y utilizado en la medida justa, es el mejor remedio para disipar tensiones, resolver situaciones y facilitar el trato y las relaciones humanas. De todo esto se deduce que puede ser un buen aliado en la divulgación científica.

Así lo han entendido grandes divulgadores como Isaac Asimov, capaz de escribir de los temas más difíciles como si estuviera tomando un café con el lector, mezclando anécdotas divertidas que le acababan de pasar con extraños fenómenos químicos, físicos o sobre importantes periodos de la Historia o la Biblia. Habla de las cartas que le envían sus lectores, o de un sonado resbalón sobre una placa de hielo en la calle y a partir de ahí empieza a explicarnos las propiedades más extrañas del agua. Hawking, Penrose, Sheldon L. Glashow, Michio Kaku, Feynman , o kip S. Thorne, y otros tantos, en mayor o menor medida también emplean el humor, más o menos fino, para desdramatizar la enseñanza de conceptos, a veces, bastante complicados. Emplean dibujos graciosos e impactantes, versos burlones , formas de hablar arcaicas, anécdotas, cualquier recurso es bueno para conseguir quitar hierro y solemnidad a las explicaciones sobre los
principios fundamentales de la ciencia.











En nuestro país, Jorge Wagensberg es un notable ejemplo del tandem humor- ciencia. Es uno de nuestros grandes científicos, físico, profesor de Teoría de los Procesos Irreversibles en la Facultad de Física de la Universidad de Barcelona y autor de una extensa obra de difusión científica en un montón de revistas y periódicos, ha dirigido durante muchos años el Museo de la Ciencia de la Fundación la Caixa. Sus artículos siempre son inteligentes, amenos, y destilan fino humor. Hace unos años publicó un libro representativo de lo que trato de explicar: “Ideas para la imaginación impura”. La imaginación impura a la que alude el título lo es porque nace de la mezcla de estímulos, de la promiscuidad de las disciplinas y del fuego cruzado de ideas, todo sazonado con buen humor.


Mientras la física fue más o menos intuitiva – hasta principios del siglo XX- no parecía tan necesario el humor para entenderla. Pero desde el desarrollo de la mecánica cuántica, la teoría de la relatividad y, últimamente, con la teoría de supercuerdas hay que tener buen humor para explicar y lograr entender los intrincados conceptos, normalmente lejos del sentido común. Creo que principalmente debido a ello los físicos cada vez utilizan más el humor para hacerse entender, más incluso que cualquier otro tipo de científicos. Es un buen medio para conseguirlo.




Algunos estudios recientes muestran que los jóvenes cada vez están menos interesados por la ciencia ( sondeo europeo reciente: 67% de jóvenes opinan que las clases de ciencias en el colegio son poco atractivas; 53% poco interesados por la ciencia;43% estima que las carreras científicas tienen poco valor). Utilizan la ciencia a través del móvil, el ordenador, mp3, etc, pero entender los principios que se esconden detrás de todos los artilugios que se utiliza no les suele interesar demasiado.

El cómic (*):

Más que utilizar el cómic como objeto de promoción o de divulgación de las ciencias, se puede usar favorablemente como vector de desarrollo del sentido crítico del niño o del adolescente. Es así como Jean-Philippe Devries, profesor de física, ha creado especialmente en la red, un cuestionario sobre las nociones de fuerza, masa y equilibrio basándose en las ilustraciones de Tintín.

Siguiendo la misma óptica, una edición especial de la revista Science & Vie, titulada “Tintín con los sabios, Hergé entre ciencia y ficción”, dedicó más de 150 páginas al espacio que ocupan la ciencia y los científicos en los numerosos cómics de Tintín.

A veces un solo personaje de cómic es utilizado a lo largo de una revista mensual de ciencias como en Cosinus en ediciones Faton. Este personaje dinamiza la puesta en página y despierta el interés del joven lector. En esta misma revista mensual, un folleto de cómic vuelve a tratar la vida y la obra de Richard Feynman. De esta manera el cómic se utiliza también para transmitir fragmentos de la historia de la ciencia, como hace con la conquista de la Luna la revista mensual Images DOC que edita Bayard Presse Jeune.

Debate:

Divertir enseñando ciencia sin perder el rigor necesario, he ahí la cuestión. Este tema ha abierto un debate que recoge la página de la Real Sociedad Española de Física. A la cuestión he aportado un par de comentarios en el debate.

(*) Revista Mètode de la Universidad de Valencia. Número 41.

La extraña probabilidad cuántica

Albert Einstein, refiriéndose a la mecánica cuántica, sin demasiado entusiasmo: “Estoy convencido de que Dios no juega a los dados”.


Cuando lanzamos al aire una moneda existen dos posibilidades: {que salga cara} o
{ que salga cruz}.Si al primer suceso le asignamos un valor de probabilidad que llamaremos p y al segundo un valor q, ocurre que, en este caso, p = q = 1/2 . Lo que que significa que para un número suficientemente alto de lanzamientos, la mitad de las veces el resultado será cara y la otra mitad será cruz. En un suceso clásico ( no cuántico), como este, los números p y q son, en general, fracciones menores de la unidad. La situación del lanzamiento de una moneda podría describirse mediante una combinación de las dos alternativas: sería : p*{que salga cara} + q*{ que salga cruz}.

En el ámbito cuántico, las cosas obedecen a leyes probabilísticas algo diferentes. Los números p y q dejan de ser fracciones para convertirse en números imaginarios (una parte real b más otra parte imaginaria con raíz cuadrada de –1) y ya no se llaman probabilidades, sino amplitudes de probabilidad, o simplemente amplitudes.


Los sucesos, mientras permanecen en ese estado puramente cuántico, están regidos por las amplitudes de probabilidad que tendrán la forma: z = a + b i ( siendo i la raíz cuadrada de –1).

Para hallar la probabilidad real cuando el suceso pasa al ámbito clásico se debe hallar el módulo al cuadrado de este número complejo, que es el cuadrado de la parte real más el cuadrado de la parte imaginaria:
| z | ² = a² + b² ( se lee módulo al cuadrado de z).

En teoría clásica de probabilidades, cuando queremos representar la situación de lanzar la moneda y la posibilidad de que salga un suceso o el otro, de forma indiferente escribimos: p*{que salga cara} + q*{ que salga cruz}. En este caso, en que la suma de probabilidades da 1, estaremos representando un suceso cierto ( probabilidad máxima = 1).

Si en dos tiradas exigimos que salga cara en la primera y cruz en la segunda, la representación sería:[ p*{que salga cara}] * [q*{ que salga cruz}]. La conjunción disyuntiva “o” , digamos que, se convierte en una suma, mientras que la “y” se convierte en un producto.

En el caso de las amplitudes ocurre lo mismo, pero mientras las probabilidades normales se suman de forma natural, como dos simples números fraccionarios, en las amplitudes de probabilidad la suma es vectorial, como en las fuerzas, tal como se explica en la figura.

( pinchar en la figura para verla mejor)

Ahora podemos entender más fácilmente lo que ocurre en el experimento de las dos rendijas, cuando observamos las figuras de interferencia que producen los electrones al pasar por ellas. Estas figuras obedecen a esta forma de sumarse y restarse las amplitudes de probabilidad cuánticas que afectan, en este caso, a los electrones.

En nuestro mundo cotidiano, macroscópico, las probabilidades ofrecen un abanico mucho más pobre que el presentan las amplitudes de probabilidad cuántica. Una vez más los números imaginarios nos ofrecen un poco más de luz para entender el extraño y poco intuitivo mundo cuántico.

Simetría de grupo: relatividad especial,invarianza, leyes de conservación, clasificación de las partículas elementales...

Cuando estudiaba en el instituto la teoría de grupos no tenía ni idea para que servía todo aquello, pero las representaciones de los elementos, componiéndose unos con otros mediante las diferentes operaciones que se definían, mostraban un orden sorprendente. Me habría impresionado saber que esas simetrías que presentaban y su belleza simple, puramente matemática, representa a la perfección la simetría del espaciotiempo y de las partículas subatómicas de las que estamos formados. La utilidad, aparte de la belleza, siempre es un aliciente añadido, la naturaleza suele “confundir” la una con la otra: la solución más útil y eficaz suele ser, además, la más bella. La teoría de grupos es por su sencillez, potencia y armonía una verdadera teoría NATURAL.

De forma muy simple, se habla de que existe simetría cuando se realiza una operación sobre algún objeto y este permanece invariante ( invarianza). Una esfera tiene simetría de forma ante un giro o ante un desplazamiento, es decir, sigue conservando su aspecto ante estas operaciones de simetría. Este tipo de simetrías continuas ( independiente de la magnitud del ángulo girado, o de la cantidad de la variable considerada) se encuentran, fácilmente, en la naturaleza y de ellas se desprenden leyes tan fundamentales como la conservación de la energía, tal como demostró en un importante teorema la eminente matemática Emmy Noether, a principios del siglo XX ( simetrías contínuas <--> leyes de conservación).
La idea básica de la aplicación de la teoría de grupos al mundo físico es describir, simbólicamente, estas operaciones de simetría utilizando el álgebra. Si una rotación sobre un eje 1 con un determinado ángulo la llamamos R1, R2 y R3 serán otras dos rotaciones diferentes sobre ejes llamados 2 y 3 con distintos ángulos. El producto R2xR1 se entenderá como la aplicación del giro R1 y después del giro R2. Este producto tiene tres propiedades simples pero muy importantes que se encuentran en la base de la bella teoría de grupo: asociativa [ R1x(R2xR3) = (R1xR2)xR3], existencia de identidad o elemento neutro ( rotación nula) y de inverso o elemento simétrico ( dos rotaciones dejan el objeto como la rotación nula). De estos tres simples axiomas brota la bella estructura de la teoría matemática de grupo.

Las propias leyes de transformación espaciotemporal de Einstein ( teoría de la relatividad restringida) son una generalización de las transformaciones del espacio de tres dimensiones al espacio de tres dimensiones espaciales más el tiempo ( espaciotiempo de Minkowski). Eugene Wigner, en 1939 escribió un artículo demostrando que cuando se aplicaba la condición algebraica de grupo de simetría a una descripción matemática del mundo, automáticamente se presuponía que se cumplirían los principios de relatividad especial y, además, las partículas elementales podían clasificarse con sencillez.


Las partículas se podían clasificar por el valor de su masa en reposo ( fuese o no cero) y por una propiedad, puramente cuántica, su espín – una especie de rotación intrínseca- cuyo valor en unidades especiales referenciadas a la constante de Plank, sólo puede ser de valor entero 0,1,2,3 ... o fraccionario 1 /2 , 3/2, 5/2, etc.
Las partículas con espín entero son llamadas bosones y las de espín fraccionado fermiones. Esta clasificación es de gran importancia porque según la clase de giro o espín que presenten las partículas sus reacciones son completamente diferentes.Los bosones son partículas de “fuerza” y los fermiones de “materia”, los primeros pueden ocupar el mismo estado cuántico y para los segundos eso es imposible .

De tres simples axiomas brota la bella estructura de la teoría matemática de grupo.


FIGURAS.- Primera: Representación de un grupo sencillo de cuatro elementos con leyes de composición interna (+) y (x), llamadas así porque al aplicarlas a sus elementos el resultado sigue perteneciendo al grupo ( "i" es la ráiz cuadrada de -1).Este grupo por ser conmutativo ( AxB =BxA), se llama abeliano o conmutativo. El elemento neutro del grupo es el +1, y el simétrico de -1 es -1, el de i es -i, etc.Segunda: El matemático N. Abel , genial introductor de la teoría de grupos, de trágica y temprana muerte a los 26 años. Tercera: Ilustración sobre Einstein/ teoría relatividad especial. Cuarta: Representación bosón-fermión.

Para saber más : Excelente artículo de Astrocosmo.

Enamorarse de la ciencia

Recientemente, ha estado en España Gerald Holton, profesor de física e historiador de la ciencia en Harvard, un verdadero especialista en Einstein, hasta tal punto que fue la persona elegida por la familia del científico para clasificar toda su documentación, después de su muerte. En la entrada de 18/6/06 , Ciencia/tecnología e imaginación, resumí una entrevista suya a la revista Mètode de la Universidad de Valencia.


En su última visita ha concedido una entrevista al periódico el El País. Le preguntaron, cuál es la característica esencial de un científico y Holton respondió: "Tal vez mis colegas sonrían, pero creo que igual que algunas personas están enamoradas del dinero y otras se enamoran del arte -ayer estuve en uno de sus maravillosos museos: el Prado, y es extraordinario-, los científicos están enamorados de la química o de la física o de las matemáticas... El científico se enamora muy joven y deja todo de lado por ese amor. Stephen Jay Gould decía que la ciencia significa que al final del día, en el laboratorio, sabes que el 99% del tiempo de trabajo ha sido tiempo perdido, y encima todavía tienes que limpiar las jaulas de los ratones. La ciencia es una actividad que exige muchísima dedicación y tiempo".

En el periódico, el titular de la entrevista decía :” Los científicos están enamorados de la química, de la física o de las matemáticas...”. Poco después, cuando he comprado el último y monumental libro de Roger Penrose “ El camino a la realidad ”, una guía completa de las leyes del universo, me ha llamado, poderosamente la atención la dedicatoria del mismo a su querido profesor Dennis Sciama (también profesor de Stephen Hawking) : ”A Dennis Sciama, que me mostró la emoción de la física”.


Hace muy poco, he vuelto a releer el formidable ensayo de Isaac Asimov “ El electrón es zurdo”. Al comienzo del mismo dice, entre broma y serio:”Por un lado, mi objeto y mi pasión, aun en mis novelas, es explicar. En parte es por instinto misionero por lo que anhelo conseguir que mis lectores vean y entiendan el Universo, como yo lo veo y entiendo, para que puedan gozarlo como yo.”

Amor, emoción, gozo por la ciencia.

Y en muchas ocasiones hace falta verdadero amor. Por ejemplo, para seguir en España en el puesto de científico becario hasta los 40 años, después de grandes esfuerzos y una gran y costosa preparación. Recientemente, Francisco Tomás, rector de la Universidad de Valencia hacía unos comentarios interesantes, a la revista Mètode de la Universidad ( número 50 ), sobre el estado actual de la ciencia:” En estos momentos hay una regresión a escala mundial del interés de los jóvenes por cursar carreras científicas, es un hecho muy inquietante”... “ Existe una intensa dedicación de los investigadores en producir conocimiento, pero esta producción ha dejado muy al margen la necesidad de difundirlo en la sociedad: el hecho de realizar una investigación competitiva, publicando en revistas de alta exigencia, ha dejado paradójicamente un poco de lado la divulgación de nuestro trabajo. Se ha producido un desfase, hay muy pocos comunicadores de la ciencia y también hay muy pocos científicos que tengan ese interés por la difusión...”

Y eso, la divulgación, es esencial para crear el tejido social necesario para que exista una “cantera” de futuros científicos. Sólo se consigue esa “cantera” transmitiendo la emoción por la ciencia, como decía Roger Penrose, y desde luego, creando las condiciones dignas para ejercerla. Hacen falta las dos cosas.

¿Universo holográfico?

Los resultados teóricos relativos a la entropía de los agujeros negros llevan a concluir que el universo podría ser un inmenso holograma. Jacob D. Bekenstein.

Del estudio de las propiedades de los agujeros negros se han deducido los límites absolutos que acotan la información que cabe en una región del espacio. Teniendo en cuenta que esos límites dependen de la materia y energía contenida en ese espacio es asombroso que se pueda deducir un límite sin conocer ni siquiera , con absoluta certeza, el último componente de la materia ( se cree que los quarks y los electrones son excitaciones de supercuerdas que deben ser los entes fundamentales, pero no se descartan niveles más bajos).

La clave está en la entropía, en 1877 , Ludwing Boltzmann la caracterizó como el número de estados microscópicos distintos ( N) en los que pueden hallarse las partículas que componen un trozo de materia de forma que siga pareciendo el mismo trozo desde un punto de vista macroscópico.

Las dos entropías: Cuando el matemático Claude E. Shannon buscó una manera de cuantificar la información contenida en un mensaje, la lógica le llevó a una fórmula que tenía el mismo aspecto que la de Boltzmann. Después se vio que la entropía termodinámica y la de Shannon son conceptualmente equivalentes: el número de configuraciones que se cuentan en la entropía de Boltzmann refleja la cantidad de información de Sannon que se necesitaría para realizar cualquier configuración determinada.

Se pensaba que cuando caía la materia en un agujero negro desaparecía también con ella su entropía, pero Demetrious Christodoulou ( 1970) y Stephen W. Hawking demostraron que en el proceso de fusión de dos agujeros negros, nunca decrecía el área total de los horizontes de sucesos. A partir de estos estudios y del posterior descubrimiento de que los agujeros negros emiten radiación , precisamente llamada radiación de Hawking ( 1974) ser su descubridor, se determinó la constante de proporcionalidad entre la entropía de un agujero negro y el área del horizonte: La entropía del agujero negro es exactamente una cuarta parte del área del horizonte de sucesos medida en áreas de Plank ( 10 ^–66 centímetros cuadrados). Es como si la entropía, en cuanto medida de información, estuviese escrita sobre el horizonte de sucesos, de suerte que cada bit ( cada 0 ó 1 de la codificación digital) correspondiera a 4 áreas de Planck.

Este sorprendente resultado tiene una explicación natural si es cierto el principio holográfico propuesto en 1993 por el Premio Nobel Gerard `t Hooft, de la Universidad de Utrech, y elaborado por Leonard Susskind. Sobre esta teoría, Juan Maldacena, de la Universidad de Harvard, en un reciente artículo de enero del 2006, en Investigación y Ciencia, afirma que: “ La fuerza de la gravedad y una de las dimensiones espaciales quizá procedan de las peculiares interacciones, entre partículas y campos, existentes en un espacio con menos dimensiones”.



La descripción tridimensional con ley de gravedad sería equivalente a la descripción holográfica sin gravedad y en dos dimensiones, de modo que un determinado cálculo demasiado difícil en una descripción puede resultar trivial en la otra. A pesar de su radical diferencia, las dos teorías describirían por igual todo lo que vemos y cualquier dato que pudiésemos recoger sobre el funcionamiento del universo.


Un holograma es un objeto bidimensional que codifica toda la información que describe la imagen tridimensional. Nuestro Universo tridimensional podría estar codificado en una superficie que lo contiene, como una especie de inmenso holograma. Los experimentos de física de partículas de altas energías, según Juan Maldacena, quizás hayan encontrado ya indicios de la validez de este principio.


Nota final: En el post sobre los condensados de Bose–Einstein, me llamó la atención un artículo del Dr. Fernando Sols de la Universidad Complutense. En él hablaba de separar un condensado de varios millones de átomos en dos partes tratando de que siguieran estando en coherencia cuántica. Le comenté, por correo, que con este tipo de “superátomos” que son los condensados de B-E se podría hacer un experimento sobre el principio holográfico. Me contestó muy amablemente, aclarándome las dificultades que entrañaría mantener la coherencia de las dos partes del condensado. Si se consigue la coherencia entre las dos partes del condensado, nos encontraríamos con la paradoja de que en cada parte del condensado no tendremos la mitad de los átomos, sino que todos los átomos estarían a la vez en las dos partes. Aunque difícil, esta podría ser una vía interesante de constatación del principio holográfico.

Investigación y cienca. Octubre-2003 y enero-2006.

Una fórmula maravillosa

Desde que la vi no la he podido olvidar... Relaciona los números imaginarios ( i = raíz cuadrada de ( –1)), con las potencias ( número e y logaritmos neperianos ) y con las funciones trigonométricas. Me ha permitido recordar, sin esfuerzo, fórmulas trigonométricas como la del seno o coseno de una suma de ángulos, del ángulo doble o mitad, y calcular, con facilidad, derivadas de funciones trigonométricas.


Nos la podemos encontrar en cualquier sitio, en cualquier expresión matemática pura o relacionada con algo tan prosaico como las relaciones de impedancias en un circuito de corriente alterna. En la función de onda de la mecánica cuántica o en cualquier expresión de naturaleza ondulatoria o periódica. En la técnica, en la física o en las matemáticas más abstractas ( Roger Penrose reflexiona– en su último libro,en el capítulo sobre las diferenciales complejas - lo que habría disfrutado Euler con todas las maravillas de su fórmula y de los números imaginarios ).

La fórmula de Euler fué demostrada por primera vez por Roger Cotes en 1714, y luego redescubierta y popularizada por Euler en 1748. Es interesante notar que ninguno de los descubridores vió la interpretación geométrica ( circunferencia en el plano complejo): la visión de los números complejos como puntos en el plano surgió unos 50 años mas tarde con Caspar Wessel, y d'Argaud.

En la figura, para el cálculo de la impedancia, el eje imaginario representa la reactancia, resultado de la resta entre la parte inductiva ( bobinas ) y la parte capacitiva ( condensadores). El ángulo ( phi ) que forman la impedancia con el eje real de la resistencia pura es sumamente importante en la industria, su coseno es lo que llamamos el factor de potencia que mide, en cierto modo, la eficiencia de un circuito. Para un ángulo grande la reactancia asociada es grande y obliga a las compañías eléctricas a suministrar una potencia reactiva adicional y a la industria a pagar un consumo innecesario. Este ángulo se corrige añadiendo baterías de condensadores que ofrecen una reactancia de signo contrario a la presentada por los motores industriales.

Lo tiene todo, es sencilla, bonita, elegante y útil, muy útil. Sin duda es una fórmula maravillosa.

Polvo fractal con dimensión entera

Como comentaba en el post sobre el “Vacío cuántico, vacío fractal ”, la existencia del cuanto de acción ha destruido por completo la propia noción de trayectoria clásica.
Laurent Nóttale complementó la definición de Richard Feynman (1965) y A. Hibbs sobre las trayectorias virtuales típicas de una partícula cuántica, indicando que los caminos cuánticos posibles son, en número infinitos, y todos son curvas fractales caracterizadas por una propiedad geométrica común: su dimensión fractal es 2.

En algunos foros he leído que no se entendía bien lo de la dimensión fractal entera, en este caso 2, pero tal como indicaba en la expresión general de la dimensión fractal:

Dimensión fractal = dimensión topológica + factor dimensional

( El factor dimensional, siempre positivo, es tanto mayor cuanto más irregular es el fractal: indica la capacidad de ocupar más espacio del que indica su propia dimensión topológica)

Si el factor dimensional es entero, también lo será la dimensión fractal. Eso es lo que ocurre con las trayectorias virtuales en mecánica cuántica y también en una serie de fractales típicos, como puede ser el fractal del movimiento browniano en un plano ( dimensión fractal 2) o la curva de Peano ( dimensión fractal 2) que tiene más de 100 años de existencia.


Si una curva clásica tiene dimensión topológica 1, cuando hablamos de curvas fractales con una dimensión entre 1 y 2 estamos indicando que son capaces de ocupar parte del plano. Y es precisamente esa capacidad la que viene expresada por el factor dimensional. En el caso de la curva de Peano o del movimiento browniano, en el límite, ocupan todo el plano, de ahí que su dimensión fractal sea 2 , la propia dimensión del plano.


Como ejemplo, todavía más llamativo, observamos en la figura un fractal clásico ( el primero que se conoce), el polvo de Cantor que toma toma su nombre de Georg Cantor que en 1883 lo utilizó como herramienta de investigación para una de sus principales preocupaciones: el continuo.






A partir de una recta se le van quitando los segmentos centrales hasta conseguir una serie infinita de puntos aislados, de ahí el nombre de polvo. Si restablecemos de forma escalonada el segmento que antes le quitábamos, el nuevo fractal sigue teniendo estructura quebrada y autosemejante , pero ahora en lugar de tener una dimensión fractal igual a log 2/ log 3 tiene una dimensión entera: log 3/ log 3 =1. Nos ayuda, también, a entender como se calcula, de forma práctica, la dimensión fractal de una figura.


Esta otra figura es una síntesis de dos de los fractales clásicos, Koch y Cantor, y nos ayuda de forma intuitiva a entender el cálculo de su dimensión fractal. En la figura original de Koch, sobre los segmento A1-B1-D1-E1 se construye la figura que forman los segmentosA-B-C-D-E. Su dimensión fractal es log 4/ log 3 ( cuatro segmentos sobre tres). En la nueva construcción se ha sustraido 1/4 de cada uno de los segmentos superiores para dejar 4 segmentos de longitud 3/4: al final son 3 sobre 3 ( log 3/ log 3 = 1).

Se pueden construir infinidad de fractales con dimensión entera y, precisamente, esa irregularidad que representa una dimensión fractal entera en un fractal creo que nos ayuda a entendelos mejor.

La aventura de la ciencia: Pierre André Méchain

Detrás de infinidad de gestos cotidianos, como la medida del mueble del salón, del hueco de la escalera o del último estirón que ha dado la pequeña de la casa, puede haber grandes historias y aventuras que desconocemos, personas que han dedicado su esfuerzo y, en ocasiones su vida, la mayoría de las veces de forma anónima.Una de estas historias llevó a sufrir y morir en tierras españolas al más alto responsable de la astronomía francesa de principios del siglo XIX : Pierre André Méchain, director del Observatorio de París y presidente del Bureau des Longitudes .

El 19 de marzo de 1791 la Academia de las Ciencias de Paris aprobó, con el voto de Méchain, que el metro, la nueva medida que la Francia revolucionaria quería dar al mundo, sería la diezmillonésima parte del cuadrante de meridiano terrestre. La mayor empresa científica realizada hasta ese momento estaba en marcha, la medida de un arco de meridiano comprendido entre Dunkerque, al norte de Francia, y Barcelona iba a dar el valor de la nueva unidad con la mayor aproximación posible.

A comienzos de 1792 se emprenden los trabajos. El arco de meridiano que se debía medir se dividió en dos partes: el primero ( Dunkerke-Rodez), ya medido anteriormente, se volvería a medir y el tramo Rodez-Barcelona, el más difícil, quedaría a cargo de la persona más experimentada, Pierre André Méchain. La técnica a emplear sería la de la triangulación geodésica, se trazaría una cadena de triángulos, el vértice de los cuales serían montañas situadas a lo largo del meridiano.

Méchain decidió empezar por la parte española. Después de pedir el permiso y la colaboración correspondientes al rey de España Carlos IV, llegó a Barcelona en julio de 1792. Poco después los colaboradores españoles le sugieren que el arco acabe en Mallorca, en lugar de acabar en Barcelona, de esta forma, su mitad se situaría más exactamente sobre el paralelo 45 y comportaría ciertas ventajas matemáticas. En diciembre, su colaborador José González, capitán del bergantín Corzo, pasó a Mallorca para reconocer las montañas más convenientes y encender fuegos en las cimas para que Méchain comprobara si era posible la medida de un gran triángulo sobre el mar, operación nunca antes realizada ( los fuegos permitían hacer las mediciones de noche, cuando las neblinas superficiales disminuyen), pero, finalmente, los instrumentos de que disponían no lo permitieron, la óptica de los mismos no era suficientemente potente.

En enero de 1793, Luis XVI es guillotinado en Paris y poco después, en marzo, estalla la guerra entre España y Francia . A Méchain se le permite seguir con sus medidas que acaba en ese mismo año, pero no se le dejó volver a su país hasta 1794. Aquejado de fuertes depresiones tardó tres años más en hacer sus últimas medidas y, finalmente en agosto de 1798 se reune con Jean Baptiste Delambre, que había medido el resto del arco de meridiano, para revisar sus cálculos. El 22 de junio de 1799 se firmó el informe final por el primer cónsul Napoleón Bonaparte, había nacido la unidad de medida universal.


Sin embargo, la aventura del metro no había acabado, el 31 de agosto de 1802 el Bureau des Longitudes decide continuar con las operaciones geodésicas en España. Aunque finalmente es Méchain quien será el director del trabajo, muchos de sus colegas habrían preferido a alguien más joven. El 5 de mayo de 1803, Méchain vuelve a Barcelona, pero en esta ocasión su viaje iba a ser una pesadilla que acabó con su trágica muerte casi año y medio después.
Las reticencias que había desencadenado la reciente guerra, las trabas burocráticas en España, que retrasaron los medios materiales necesarios, y las contraórdenes del propio Bureau des Longitudes hicieron pasar al astrónomo por multitud de penalidades que no acabaron hasta que contrajo el paludismo por tierras valencianas . En la sierra Espadán se manifestaron los primeros síntomas, entonces escribe su última carta:” ... Esta desgraciada misión, el éxito de la cual está todavía tan lejano y resulta más que incierto, provocará muy probablemente mi perdición y, lo que es peor todavía, la de mi familia, mi tumba y la de mi honor...”.

Dos meses después, el 20 de septiembre de 1804, moriría entre los brazos de su amigo, Fausto Vallés y Vega, Barón de Pobla Tornesa. Una aventura que duró más de 13 años y costó la vida a su principal protagonista.


Nº43 Revista Mètode "La ciència i la Tragèdia, Pierre André Méchain (1744-1804), Antoni Ten. Universidad de Valencia.

Vacío cuantico, vacío fractal

El vacío estable y absoluto de Newton, con trayectorias continuas y determinadas, ha dejado paso al vacío cuántico asociado a unas extrañas trayectorias (*) discontinuas y fracturadas, llamadas por ello trayectorias fractales ( no son propiamente trayectorias). La existencia del cuanto de acción o constante de Planck ( se llama acción al producto de una energía por un tiempo ), base de la física cuántica, es la causa de ese cambio fundamental, y de otros muchos, con profundas consecuencias. Mediante la geometría fractal, este nuevo marco nos ofrece nuevas e interesantes perspectivas.


La existencia del cuanto de acción supone, realmente, la desaparición del vacío como tal. La mínima energía posible en el espacio (fluctuaciones cuánticas) deja de ser cero para pasar a depender del inverso de la distancia considerada. A la menor distancia posible (longitud de Planck = 10^-35 metros) , se le asocia una energía considerable, equivalente a una masa de 0,00002 gramos, y si mantuviéramos la misma relación, la masa correspondiente a un metro sería del orden de 1,2 x10²⁴ toneladas. Pero la propia existencia del mínimo cuanto de acción - principio de incertidumbre - determina que las fluctuaciones de energía del vacío queden acotadas, y sean cada vez menores conforme aumenta la distancia. Para las distancias macroscópicas, cotidianas para nosotros, son prácticamente nulas.

El vacío plano y estable ha dejado paso a un vacío cuántico modulado por sus fluctuaciones de energía que le dotan de una estructura fractal, discontinua. Dicha estructura, aparentemente extraña en la teoría, es por el contrario de lo más común en el mundo real. Cualquier superficie , por ejemplo, por lisa que nos parezca, al examinarla con un aumento progresivo la observaremos cada vez con mayores imperfecciones, hendiduras y discontinuidades. Ocurre con cualquier objeto del mundo real, la esfera, el cubo, o la línea perfecta no existen . No dejan de ser simplificaciones convenientes a las que asociamos conceptos sencillos y fáciles de manipular. Sin embargo las simplificaciones nos pueden ocultar detalles decisivos.

Supongamos que queremos recorrer, a pie, la distancia entre dos puntos determinados. Si la medimos sobre un plano, en línea recta, encontraremos una distancia determinada que se verá ampliamente superada cuando hagamos el trayecto en la realidad. Tendremos que subir, bajar, desviarnos un montón de veces de la trayectoria teórica preestablecida sobre el plano.En la realidad, habremos seguido una trayectoria fractal. Si ese mismo viaje lo hubiera hecho una hormiga, su trayectoria habría sido mucho más irregular que la nuestra y la distancia a recorrer mucho mayor , porque el paso de la hormiga es considerablemente menor que el humano.

Dimensión fractal = dimensión topológica + factor dimensional

( El factor dimensional, siempre positivo, es tanto mayor cuanto más irregular es el fractal)

En una línea perfecta eso no ocurre, pero en una trayectoria fractal si. Una línea teórica tiene dimensión topológica o aparente igual a la unidad, pero para una línea fractal existe un factor dimensional positivo , que se suma a la dimensión aparente para constituir la que llamamos dimensión fractal. Conforme sea más discontinuo e irregular un fractal mayor será este factor y , por tanto, mayor su dimensión fractal.


(En la figura ( representación del vacío cuántico), los trazos más anchos se corresponden con fermiones( quarks, electrones...) y sus antipartículas, mientras que los trazos más finos corresponden a bosones (gluones, fotones, W+, W-, Z0,...). En lo concerniente al color de los quarks y gluones, se corresponden con la carga de color de los mismos mientras que las partículas insensibles a la interacción fuerte aparecen en blanco o gris.)


(*) De hecho, no son propiamente trayectorias, las trayectorias clásicas no existen en mecánica cuántica .Concretamente, su dimensión fractal es 2 , pues por curioso que parezca existen fractales con dimensión entera.


(Reedición, ampliada, del post de fecha 06/06/2006 )

Premio Príncipe de Asturias de Investigación Científica

El físico español Juan Ignacio Cirac Sasturain, que dirige el departamento de óptica cuántica del Instituto Max Planck de Alemania(*), ha sido galardonado con el Premio Príncipe de Asturias de Investigación Científica. Nacido en 1965, se convierte en el ganador más joven en esta categoría.

Cirac Sasturain, natural de la localidad barcelonesa de Manresa, llegó a las últimas votaciones junto a las candidaturas conjuntas de los biólogos Ginés Morata y Peter Lawrence y de los químicos Avelino Corma y James Fraser Stoddar, a las que se impuso finalmente.

En el acta del jurado, presidido por el bioquímico Julio Rodríguez Villanueva, se le hace merecedor del premio "por su liderazgo mundial en la propuesta y desarrollo de la información cuántica, una nueva ciencia del siglo XXI que surge de combinar dos de las creaciones más notables de la ciencia del XX". Es decir, "de un lado la física cuántica, que explica el comportamiento de la materia a nivel atómico y subatómico, y del otro la teoría de la información, que describe el procesado, almacenamiento y transmisión de datos".

Añade que "el profesor Cirac es un referente internacional que ha producido algunas de las ideas más originales y brillantes tanto en el campo de la información cuántica como en el de la teoría cuántica de la luz y la física atómica". ( En la figura, qubits en nanotubo de carbono)

El jurado concluye señalando que "sus contribuciones están siendo decisivas para el desarrollo de comunicaciones completamente seguras, gracias a métodos de cifrado cuántico ( encriptación cuántica), y para la construcción de ordenadores potencialmente capaces de realizar en segundos cálculos que sobrepasan los límites actuales de la supercomputación" ( computación cuántica/ paralelismo cuántico) .

La computación mecanico-cuántica se basa en una propiedad misteriosa de la mecánica cuántica : la coherencia cuántica. En un ordenador actual la información se codifica en ceros (0) y unos (1). El estado de un bit ( unidad mínima de información) sólo puede encontrarse en (1) o en (0).

En un ordenador cuántico la unidad mínima de información es el qubit, un estado entrelazado, mezcla de los dos estados a la vez, de forma coherente. Para visualizarlo podemos imaginar una esfera, en el polo norte situariamos el (1) y en el polo sur el (0) : el qubit representaría cualquier punto de la esfera como una combinación de los dos estados a(0) + b(1). ( El (0) y el (1) constituirían lo que en música son los tonos puros musicales, en cambio, una superposición de (0) y (1) sería un acorde).

La potencia de la computación cuántica se basa en la coherencia que permite un efecto de paralelismo : Colocamos todos los qubits de entrada en idéntica superposición de ceros y unos, todos iguales. La computadora se encuentra entonces en otra superposición de todas las entradas posibles. Si hacemos pasar esta entrada a través de un circuito lógico que ejecute un determinado cómputo, el resultado es una superposición de todos los posibles resultados de ese cómputo: la computadora efectúa a la vez todos los cómputos posibles.

Símil musical: Una computadora cuántica que realice un cómputo ordinario, en el que no haya superposición de bits, genera una secuencia de ondas ( mecanico-cuánticas) análogas al sonido de un "cambio de repique" de los campanarios, en que las campanas se tañen una por vez. Un cómputo realizado en modo cuántico paralelo viene a ser como una sinfonía, su sonido corresponde a una multitud de ondas que se interfieren entre sí.

(*) La buena noticia es que tengamos científicos de esta talla, la mala noticia es que no trabajen en España. La endogamia de nuestra Universidad, seguro que no ayuda a solucionar el problema.
Fuentes: Agencia EFE y Revista Investigación y Ciencia TEMAS 10: "Misterios de la física cuántica" (4º trim.1997)

El efecto mariposa, un atractor extraño

El orden lleva asociado un grado importante de predicción, al caos le sucede lo contrario. Los sistemas lineales, representan el orden, son predecibles y cómodos de manejar, de ahí nuestra tendencia a generalizarlos. Ante un sinfín de situaciones generalizamos, proyectamos los datos del presente para tratar de averiguar un comportamiento futuro y casi siempre nos va bien. Pero existen sistemas que se resisten: pequeñas variaciones, incertidumbres, en los datos iniciales desembocan en situaciones finales totalmente descontroladas e impredecibles. Son los llamados sistemas caóticos ( En la figura, atractor extraño "poisson_saturne" hecho con el programa Chaoscope).


Para estudiar estos sistemas se requiere de una metodología diferente. Su estudio se realiza en el llamado espacio de fases, un espacio abstracto en el que se representan todas las variables dinámicas del sistema. Por ejemplo, un péndulo simple ideal se vería representado por dos variables, la velocidad y la posición de la masa suspendida. Su representación podría hacerse, por tanto, en el plano y sería una circunferencia. Cada punto de la misma representaría dos cantidades, la velocidad y la posición, en ese momento.


Esa figura en el espacio de fases, a la que se aproxima el fenómeno estudiado, se le llama su atractor. En los sistemas no caóticos el atractor suele ser un punto, una circunferencia, una figura geométrica conocida, pero en los sistemas caóticos presenta una forma “extraña”, de ahí que reciba el nombre de “atractor extraño”, con una dimensión fraccionaria o fractal ( En la figura, atractor de Lorenz, en 3D, con el programa Chaoscope).

El primero de éstos fue hallado, por casualidad, por el meteorólogo Edward Lorenz cuando trataba de encontrar un modelo matemático que permitiera predecir el comportamiento de grandes masas de aire. Consiguió ajustar el modelo a sólo tres variables que indican como cambian la velocidad y la temperatura del aire a lo largo del tiempo (atractor de Lorenz).


Después de haber estudiado el modelo, volvió a introducir los datos iniciales - esta vez con menos decimales- y el resultado que obtuvo fue completamente diferente del anterior. Cuando reflexionó sobre los resultados se dio cuenta que el sistema era extremadamente sensible a las condiciones iniciales: pequeñas perturbaciones en los datos de partida tienen una gran influencia sobre el resultado final. Sus ecuaciones captaban la esencia de la verdadera atmósfera. “Aquel primer día ( invierno de 1961) decidió que los pronósticos amplios estaban condenados a la extinción”. Pero vio más que azar en su modelo del tiempo: una fina estructura geométrica, orden disfrazado de casualidad.


Para explicar de una manera gráfica – y exagerada - la cuestión se le ocurrió que el simple aleteo de una mariposa, que no se hubiera tenido en cuenta en los datos iniciales, podía modificar una predicción hasta hacerla totalmente inviable después de un determinado tiempo.


Sobre el efecto mariposa se han escrito cientos de artículos, novelas, canciones y se han hecho películas. Recientemente he leído un artículo de Enrique Dans, profesor del Instituto de Empresa, en el que compara el “ecosistema de Internet” con los sistemas no lineales y complejos como el tiempo atmosférico:” Las variables en juego ( en Internet) no son tantas: si en el clima hablamos fundamentalmente de velocidad y temperatura del aire, en Internet hablamos de visitas, vínculos y cuestiones afines. Pero el posible impacto de una variación infinitesimal en medición de las variables de origen puede tener un impacto brutal en los resultados finales,...” . “ Criterios que todo el mundo, aparentemente, da por buenos, como el sacrosanto PageRank de Google, la cuenta de vínculos entrantes de una página web que lleva a cabo Technorati o los rankings de popularidad de Alexa son medidas completamente burdas, groseras, carentes de inteligencia, que responden únicamente al deseo e intentar reducir la incertidumbre, pero que lo hacen, en general, bastante mal.”


En este sentido nos encontramos en la era anterior al descubrimiento del efecto mariposa, utilizamos métodos lineales para tratar de analizar los sistemas complejos, no lineales, en donde las realimentaciones de todo tipo, y a todos los niveles, son la propia esencia del sistema. Necesitamos conocer "el atractor extraño de Internet".

Para saber más:"Caos,La creación de una ciencia", de James Gleik. Seix Barral. Barcelona 1988. Un magnífico libro

Los físicos y la metafísica

El post anterior acababa con unas reflexiones filosóficas del eminente físico Michio Kaku sobre el sentido de la vida. Aunque a algunos no les guste demasiado, los físicos son también personas y suelen pensar, más de lo que parece, en temas trascendentales. Esa aproximación a la persona fue la que me decidió a acabarlo así.

Por otra parte, en el libro de Michio Kaku, poco antes de esas reflexiones se citan unas palabras del propio Stephen Hawking ( cuando creía que la gran unificación de las interacciones fundamentales estaba próxima a llegar, al final del siglo XX ): “Si descubrimos una teoría completa, con el tiempo debería ser comprensible en sus principios generales para todo el mundo, no sólo para unos pocos científicos. Entonces todos nosotros, filósofos, científicos y simples personas normales, deberíamos ser capaces de tomar parte en la discusión acerca de la cuestión de por qué nosotros y el universo existimos. Si encontráramos la respuesta a ello, sería el triunfo final de la razón humana- pues entonces conoceríamos la mente de Dios.

Bien conocida es, también, la famosa frase atribuída a Einstein, sobre la mecánica cuántica: “ Dios no juega a los dados”. Otra frase suya relacionada con su apreciación de las claves que llevan al entendimiento de las leyes físicas decía: ”Dios es sutil, no malicioso” ( es impresionante). Finalmente, en otra de sus reflexiones decía:” Creo en el Dios de Spinoza que se manifiesta en la ordenada armonía de lo que existe, no en un Dios que se preocupa del destino y de las acciones del ser humano”.

Roger Penrose, uno de los físico-matemáticos más eruditos y creativos del mundo roza la metafísica al ocuparse exhaustivamente del problema filosófico de la conexión “mente-cuerpo”. En su famoso libro “La nueva mente del emperador”, recorre la teoría de la relatividad, la mecánica cuántica y la cosmología persiguiendo esta trascendente cuestión. Se revela como un filósofo de primera fila, que no teme abordar problemas que los filósofos contemporáneos despachan calificándolos de sin sentido.

El eminente físico David Bohm, tuvo una estrecha relación con el filósofo Krishnamurti que influyó de una manera decisiva en la formulación de su teoría física sobre el orden plegado-desplegado y el paradigma holográfico. Su interpretación “apóstata” de la mecánica cuántica.

En uno de los últimos post comentaba, también sobre este aspecto de Dirac: Para Dirac, Díos debía ser un gran matemático y con las matemáticas que conocemos nos acercamos a conocer un trocito de su creación. Curiosamente, Dirac era un gran ateo. Al respecto, Pauli escribió bromeando en sus memorias: "Si entiendo correctamente a Dirac, él dice: no hay Dios, y Dirac es su profeta".

Paul Davies, profesor de matemáticas aplicadas en el King`s College de Londres y catedrático de física teórica en la Universidad de newcastle, tiene todo un libro dedicado a "Dios y la nueva física".

Finalmente, creo que los físicos que han llegado a entender en profundidad la armonía y belleza que encierran las leyes naturales no pueden dejar de pensar en una cierta transcendencia, crean o no crean en Dios. Sienten que la grandeza de los misterios que tratan de sondear traspasan lo puramente físico.

Metafísica, título dado por el filósofo peripatético Andrónico de Rodas al conjunto de 14 libros del filósofo griego Aristóteles que, cuando fueron recopilados y editados por aquél (c. 70 a.C.), se encontraban “después de (la) física” (en griego, meta (ta) physica). Su contenido versa sobre lo que el propio Aristóteles definía como primera filosofía: el estudio del ser (aquello más general y común que comparten todas las entidades y cuyos rasgos son universales). Es una de las principales obras de la antigua filosofía griega y constituye una de las más influyentes de toda la historia de la filosofía occidental. Su título da nombre a una de las principales ramas filosóficas, la metafísica.

La función modular de Ramanujan y la teoría de cuerdas

La teoría de cuerdas supone que cada modo o vibración de una cuerda fundamental representa una partícula elemental distinta, y puede explicar a la vez la naturaleza de la materia y del espacio-tiempo (las partículas en lugar de ser puntuales pasan a ser unidimensionales). Es la primera teoría cuántica de la gravedad: Cuando se calcularon por primera vez las ligaduras de autoconsistencia que impone la cuerda sobre el espacio-tiempo, se observó con sorpresa que las ecuaciones de Einstein ( teoría de la gravedad) emergían de la cuerda, de hecho, el gravitón o cuanto de gravedad era la menor vibración de la cuerda cerrada.

No sabemos todavía por qué la teoría de cuerdas está definida sólo en 10 y 26 dimensiones, aunque parece seguro que esta teoría no podría unificar las fuerzas fundamentales con tan solo tres dimensiones. Las cuerdas se rompen y se forman en el espacio N-dimensional arrastrando con ellas una serie de términos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos aparecen multiplicados por el factor (N-10), lo que nos obliga a elegir N=10 para eliminarlos.

Los teóricos de cuerdas al intentar manipular los diagramas de lazos KSV ( Kikkawa-Sakita-Virasoro) creados por las cuerdas en interacción encuentran unas extrañas funciones llamadas modulares que aparecen en las ramas más distantes e “inconexas” de las matemáticas((Yutaka Taniyama ( Japón, 1927-1958) observó que cada función modular está relacionada con una curva elíptica. Esto forma la base de la conjetura Taniyama-Shimura que demostró ser una parte importante en la demostración del Último Teorema de Fermat de Andrew Wiles )). Una función que aparece continuamente en la teoría de funciones modulares se denomina función de Ramanujan, en honor al matemático Srinivasa Ramanujan, nacido en 1887 en Erode, India, cerca de Madrás.

Ramanujan, trabajando en total aislamiento ( y sin formación, toda su instrucción matemática la consiguió de la lectura de un oscuro y olvidado libro de matemáticas escrito por George Carr), fue capaz de redescubrir por sí mismo lo más valioso de cien años de matemáticas occidentales y de dejarnos una obra, que consta de 4.000 fórmulas en cuatrocientas páginas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario ni demostración. Tenía tal intuición que los teoremas simplemente fluían de su cerebro, sin el menor esfuerzo aparente. Solía decir que las diosas Namakkal le inspiraban la fórmulas en sueños.

Trabajaba en el puerto franco de Madrás, en un trabajo servil con una mísera paga, pero tenía la suficiente libertad y tiempo para seguir con sus sueños matemáticos. Después de enviar varias cartas a tres matemáticos británicos conocidos, consiguió que el brillante matemático de Cambridge Godfrey H. Hardy se diera cuenta de su inmenso genio matemático y lo trajo a Cambridge en 1914. Hardy tratando de estimar la capacidad matemática de Ramanujan, concedía un 80 al gran matemático David Hilbert, un 100 a Ramanujan y un 25 a sí mismo.


La función de Ramanujan contiene un término elevado a la potencia veinticuatro. Ese número es el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas, pues cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando se generaliza la función de Ramanujan,el número 24 queda reemplazado por el 8. Si tenemos en cuenta que se añaden dos dimensiones más al número total de vibraciones que aparecen en una teoría relativista, obtendremos 8+2, ó 10: La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer autoconsistente.

Pura geometría para explicarlo todo, el sueño de Einstein. Y las matemáticas más extrañas imaginadas por un genio, sin apenas instrucción básica, para introducirnos en una teoría de cuerdas que necesita de matemáticas que todavía desconocemos. Einstein tenía las matemáticas inventadas por Riemann para su teoría de la relatividad general, la teoría de cuerdas quizás necesite de las matemáticas, que descansan en los cuadernos llenos de teoremas sin demostrar, de Ramanujan. En el fondo, siempre, una hermosa conexión entre las ramas más distantes e inconexas de las matemáticas y la propia realidad que representan las leyes físicas.

Para saber mucho más: "HIPERESPACIO", de Michio Kaku,( 1996 CRÍTICA-Grijalbo Mondadori,S.A. Barcelona) profesor de física teórica en la City University de Nueva York. Es un especialista a nivel mundial en la física de las dimensiones superiores ( hiperespacio). Despide el libro con una palabras preciosas:”Algunas personas buscan un significado a la vida a través del beneficio personal, a través de las relaciones personales, o a través de experiencias propias. Sin embargo, creo que el estar bendecido con el intelecto para adivinar los últimos secretos de la naturaleza da significado suficiente a la vida”.

DIOS DIJO:"QUE NEWTON SEA"

Tengo sobre la mesa el viejo y manoseado libro que aparece en la figura. Lo abro por el capítulo III y leo:
“DIOS DIJO;”QUE NEWTON SEA (*)”... “ El año en que Galileo moría en su reclusión de Florencia, un niño prematuro, bautizado con el nombre de Isaac, nacía en la familia de un agricultor del Licolnshire apellidada Newton. Durante los primeros años de escuela Isaac no dio signos de su futura grandeza. Era un muchacho enfermizo, tímido, más bien retrasado en sus estudios. Lo que le sacó de este estado fue su primera riña con un compañero de la escuela que, además de ser uno de los mejores estudiantes de la clase, era muy agresivo hacia los otros muchachos. Al recibir un golpe en el vientre que le asestó este camorrista (cuyo nombre se ha perdido para la historia ), Newton le desafió a luchar y le venció a causa de su "espíritu superior y resolución". Después de haber ganado en el aspecto físico, decidió completar su victoria en la batalla de la inteligencia y, trabajando esforzadamente, llegó a ser el primero de su clase. Después de ganar otra batalla con su madre que quería dedicarle a la agricultura, entró en el Colegio de la Trinidad a la edad de 18 años y se consagró al estudio de las matemáticas. En el año 1665, Newton tomó su grado de bachiller en artes sin ninguna distinción especial."

Cuando yo tenía unos 15 años en mi primer viaje, con mis padres, a Madrid me lo compré y empecé a leerlo. Su lectura me atrapó como sólo pueden hacerlo los buenos libros a esas edades. Consiguió que imaginara la aventura de la ciencia como una aventura más, y a sus personajes como los protagonistas de los libros de piratas y aventuras.

George Gamow, en su prólogo ( Univ. De Colorado, 1 de junio de 1960) dice:” En el presente libro, he intentado seguir un camino intermedio ( entre los libros de texto y los históricos) exponiendo lo mismo el proceso de Galileo que las leyes fundamentales de la mecánica por él descubiertas o presentando mis recuerdos personales sobre Niels Bohr junto con una detallada discusión del modelo del átomo de este físico... espero que este libro servirá para que los jóvenes lectores ( y acaso algunos viejos) sientan el impulso de estudiar Física; esta es su finalidad principal.

El libro se divide en los siguientes capítulos:
I. La aurora de la Física.
II. Las edades oscuras y el Renacimiento.
III. Dios dijo:"Que Newton sea".
IV. El calor como energía.
V. La edad de la electricidad.
VI. La revolución relativista.
VII. La ley de los cuanta.
VIII. El núcleo atómico y las partículas elementales.

Este post pretende brindar a este libro y a su autor mi pequeño homenaje y el de mis posibles lectores. ( Después de esto me voy a comprar una edición moderna del libro y a retirar, a un merecido descanso, la edición super-antigua de la foto).

(*)De unos versos de Alexander Pope (1688-1744):"La Naturaleza y sus leyes yacían ocultas en la noche; Dios dijo:"Que Newton sea", y todo se hizo luz."