El Big Bang, una explosión en perfecto orden

La curvatura del espacio-tiempo se manifiesta como un efecto marea. Si caemos hacia una gran masa sentiremos que nuestro cuerpo se estira en la dirección de caida y se aplasta en las direcciones perpendiculares a aquella. Esta distorsión de marea aumenta a medida que nos acercamos, de forma que para un cuerpo que caiga a un agujero negro de varias masas solares el efecto lo destrozaría, destrozaría sus moléculas, sus átomos, después, sus núcleos y todas las partículas subatómicas que lo constituyeran. Un verdadero efecto desorganizador, y motor de desorden, de la gravedad en su máximo exponente. No sólo la materia, sino el propio espacio-tiempo encuentran su final en las llamadas singularidades del espacio-tiempo que representan los agujeros negros. Son consecuencias que se deducen de las ecuaciones clásicas de la relatividad general de Einstein y de los teoremas de singularidad de Penrose y Hawking.

Si los agujeros negros son singularidades en donde colapsa la materia y el propio espacio-tiempo, existen otro tipo de singularidades. Utilizando la dirección inversa del tiempo nos encontramos con la singularidad incial en el espacio-tiempo que llamamos Big Bang. Esta singularidad representa todo lo contrario, la creación del espacio-tiempo y de la materia. Aunque podríamos pensar que hay una completa simetría entre los dos fenómenos, cuando los estudiamos con detenimiento encontramos que no pueden ser exactamente inversos en el tiempo. La diferencia entre ellos contiene la clave del origen de la segunda ley de la termodinámica, la famosa ley que dice que :"La cantidad de entropía, o desorden, de cualquier sistema aislado termodinámicamente tiende a incrementarse con el tiempo, hasta alcanzar un valor máximo". También contine la clave de la llamada flecha del tiempo.

La entropía (o medida del desorden) en un agujero negro es elevadísima. De hecho, para hacernos una idea, la compararemos con la entropía que suponíamos que contribuía en mayor manera al total del Universo, la correspondiente a la radiación de fondo. Esta entropía, en unidades naturales, considerando la constante de Boltzman como unidad, es del orden de 10⁸ por cada barión del Universo, mientras que la entropía por barión en el Sol es del orden de la unidad. Mediante la fórmula de Bekenstein-Hawking se encuentra que la entropía por barión en un agujero negro de masa solar (en agujeros más masivos es todavía mayor) es del orden de 10²⁰ en unidades naturales.

Para un Big Crunch, o "crujido" final en que colapsara todo el Universo en un gigantesco agujero negro, la entropía por barión sería del orden de 10³¹. La existencia de la segunda ley de la termodinámica sería imposible en un universo que emergiera con ese desorbitado desorden,siguiendo una simetría temporal entre singularidades de colapso y de creación. De hecho el Big Bang fue una gran explosión en completo orden. Dio lugar a nuestro espacio-tiempo y a la materia de nuestro Universo y desde entonces ha ido aumentando la entropía, según la segunda ley, y marcando una flecha del tiempo que va desde este inicio al final del Universo.

El orden inicial, tal como apunta Penrose y se comenta en la entrada "las estrellas, fuente de orden y de baja entropía", es el responsable de todo nuestro orden actual y futuro, y de la organización que presentan nuestros organismos vivos.

Hasta tal punto fue ordenada la explosión inicial, que la distorsión destructiva a la que me refería al principio, que tiende a infinito en un agujero negro, fue igual a cero en el Big Bang. Esta distorsión del espacio-tiempo, con conservación de volumen, debida al tensor de curvatura espacio-temporal llamado Weyl, fue nula.

Comentario del autor (18-09-2007):

A diferencia de lo que ocurre en la implosión de la materia para formar un agujero negro, que es un fenómeno capaz de crear cantidades inmensas de entropía (o desorden), en el momento de la "explosión" del Big Bang la entropía fue mínima, de hecho es la única forma en que se puede dar un Universo con la segunda ley de la termodinámica. A partir de entonces la entropía no ha dejado de crecer.

Lo que ocurre es que la "explosión" del Big Bang no lo fue en el sentido que conocemos: algo que estalla en el espacio y en el tiempo, fue el propio "estallido" del espacio-tiempo. Para entenderlo se suele poner el ejemplo de un globo cuando se hincha. Debemos imaginar que la superficie del globo es el propio espacio-tiempo que se ensancha aunque de forma muy violenta, formando el propio espacio-tiempo que conocemos. No hay un centro estático de la explosión, porque todo se aleja de todo, tal como observamos en la expansión actual del Universo.

Reedición del post de fecha 26/09/2007. Un saludo amigos.

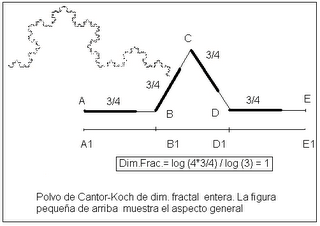
Polvo fractal con dimensión entera

Como comentaba en el post sobre el “Vacío cuántico, vacío fractal ”, la existencia del cuanto de acción ha destruido por completo la propia noción de trayectoria clásica.Laurent Nóttale complementó la definición de Richard Feynman (1965) y A. Hibbs sobre las trayectorias virtuales típicas de una partícula cuántica, indicando que los caminos cuánticos posibles son, en número infinitos, y todos son curvas fractales caracterizadas por una propiedad geométrica común: su dimensión fractal es 2.

En algunos foros he leído que no se entendía bien lo de la dimensión fractal entera, en este caso 2, pero tal como indicaba en la expresión general de la dimensión fractal:

Dimensión fractal = dimensión topológica + factor dimensional

(El factor dimensional, siempre positivo, es tanto mayor cuanto más irregular es el fractal: indica la capacidad de ocupar más espacio del que indica su propia dimensión topológica)

Si el factor dimensional es entero, también lo será la dimensión fractal. Eso es lo que ocurre con las trayectorias virtuales en mecánica cuántica y también en una serie de fractales típicos, como puede ser el fractal del movimiento browniano en un plano (dimensión fractal 2) o la curva de Peano (dimensión fractal 2) que tiene más de 100 años de existencia.

Si una curva clásica tiene dimensión topológica 1, cuando hablamos de curvas fractales con una dimensión entre 1 y 2 estamos indicando que son capaces de ocupar parte del plano. Y es precisamente esa capacidad la que viene expresada por el factor dimensional. En el caso de la curva de Peano o del movimiento browniano, en el límite, ocupan todo el plano, de ahí que su dimensión fractal sea 2 , la propia dimensión del plano.

Como ejemplo, todavía más llamativo, observamos en la figura un fractal clásico ( el primero que se conoce), el polvo de Cantor que toma toma su nombre de Georg Cantor que en 1883 lo utilizó como herramienta de investigación para una de sus principales preocupaciones: el continuo.

A partir de una recta se le van quitando los segmentos centrales hasta conseguir una serie infinita de puntos aislados, de ahí el nombre de polvo. Si restablecemos de forma escalonada el segmento que antes le quitábamos, el nuevo fractal sigue teniendo estructura quebrada y autosemejante , pero ahora en lugar de tener una dimensión fractal igual a log 2/ log 3 tiene una dimensión entera: log 3/ log 3 =1. Nos ayuda, también, a entender como se calcula, de forma práctica, la dimensión fractal de una figura.

Esta otra figura es una síntesis de dos de los fractales clásicos, Koch y Cantor, y nos ayuda de forma intuitiva a entender el cálculo de su dimensión fractal. En la figura original de Koch, sobre los segmento A1-B1-D1-E1 se construye la figura que forman los segmentosA-B-C-D-E. Su dimensión fractal es log 4/ log 3 ( cuatro segmentos sobre tres). En la nueva construcción se ha sustraido 1/4 de cada uno de los segmentos superiores para dejar 4 segmentos de longitud 3/4: al final son 3 sobre 3 ( log 3/ log 3 = 1).

Se pueden construir infinidad de fractales con dimensión entera y, precisamente, esa irregularidad que representa una dimensión fractal entera en un fractal creo que nos ayuda a entendelos mejor.

Reedición de uno de mis post clásicos. Feliz año amigos.

Dios, Hawking, los físicos y la metafísica

En este antiguo post sobre la física de dimensiones superiores recordaba unas palabras de Michio Kaku despidiendo su famoso libro "Hiperespacio": "Algunas personas buscan un significado a la vida a través del beneficio personal, a través de las relaciones personales, o a través de experiencias propias. Sin embargo, creo que el estar bendecido con el intelecto para adivinar los últimos secretos de la naturaleza da significado suficiente a la vida".

Desde entonces ha llovido mucho. Stephen Hawking hizo unas declaraciones sobre la ciencia y Dios, indicando que ya no es necesario para explicar el origen del Universo. Me han sorprendido mucho pues desde que el hombre descubrió, ya en la antigua Mesopotamia, que la naturaleza se rige por una serie de leyes más o menos complejas el papel de Dios ha dejado de ser crucial, en cierta forma. Digo en cierta forma porque ¿cómo demostramos que no ha sido Él el que ha creado esas leyes? ¿Son leyes "per se"? ¿El hecho de que lleguemos a conocerlas a la perfección hace que Dios no sea necesario para explicar el origen de Todo, ni siquiera el origen de esas leyes? La cuestión principal creo que sigue siendo la misma que para los mesopotámicos. Sobre los físicos y la metafísica paso a reeditar un antiguo post . En el post el propio Hawking llega a identificar las leyes naturales con el "pensamiento de Dios". Un saludo.

El post anterior acababa con unas reflexiones filosóficas del físico Michio Kaku sobre el sentido de la vida. Aunque a algunos no les guste demasiado, los físicos son también personas y suelen pensar, más de lo que parece, en temas trascendentales. Esa aproximación a la persona fue la que me decidió a acabarlo así.

Por otra parte, en el libro de Michio Kaku, poco antes de esas reflexiones se citan unas palabras del propio Stephen Hawking ( cuando creía que la gran unificación de las interacciones fundamentales estaba próxima a llegar, al final del siglo XX ): “Si descubrimos una teoría completa, con el tiempo debería ser comprensible en sus principios generales para todo el mundo, no sólo para unos pocos científicos. Entonces todos nosotros, filósofos, científicos y simples personas normales, deberíamos ser capaces de tomar parte en la discusión acerca de la cuestión de por qué nosotros y el universo existimos. Si encontráramos la respuesta a ello, sería el triunfo final de la razón humana- pues entonces conoceríamos la mente de Dios.

Bien conocida es, también, la famosa frase atribuída a Einstein, sobre la mecánica cuántica: “ Dios no juega a los dados”. Otra frase suya relacionada con su apreciación de las claves que llevan al entendimiento de las leyes físicas decía: ”Dios es sutil, no malicioso” ( es impresionante). Finalmente, en otra de sus reflexiones decía:” Creo en el Dios de Spinoza que se manifiesta en la ordenada armonía de lo que existe, no en un Dios que se preocupa del destino y de las acciones del ser humano”.

Roger Penrose, uno de los físico-matemáticos más eruditos y creativos del mundo roza la metafísica al ocuparse exhaustivamente del problema filosófico de la conexión “mente-cuerpo”. En su famoso libro “La nueva mente del emperador”, recorre la teoría de la relatividad, la mecánica cuántica y la cosmología persiguiendo esta trascendente cuestión. Se revela como un filósofo de primera fila, que no teme abordar problemas que los filósofos contemporáneos despachan calificándolos de sin sentido.

El eminente físico David Bohm, tuvo una estrecha relación con el filósofo Krishnamurti que influyó de una manera decisiva en la formulación de su teoría física sobre el orden plegado-desplegado y el paradigma holográfico. Su interpretación “apóstata” de la mecánica cuántica.

En uno de los últimos post comentaba, también sobre este aspecto de Dirac: Para Dirac, Díos debía ser un gran matemático y con las matemáticas que conocemos nos acercamos a conocer un trocito de su creación. Curiosamente, Dirac era un gran ateo. Al respecto, Pauli escribió bromeando en sus memorias: "Si entiendo correctamente a Dirac, él dice: no hay Dios, y Dirac es su profeta".

Paul Davies, profesor de matemáticas aplicadas en el King`s College de Londres y catedrático de física teórica en la Universidad de newcastle, tiene todo un libro dedicado a "Dios y la nueva física".

Finalmente, creo que los físicos que han llegado a entender en profundidad la armonía y belleza que encierran las leyes naturales no pueden dejar de pensar en una cierta transcendencia, crean o no crean en Dios. Sienten que la grandeza de los misterios que tratan de sondear traspasan lo puramente físico.

Metafísica, título dado por el filósofo peripatético Andrónico de Rodas al conjunto de 14 libros del filósofo griego Aristóteles que, cuando fueron recopilados y editados por aquél (c. 70 a.C.), se encontraban “después de (la) física” (en griego, meta (ta) physica). Su contenido versa sobre lo que el propio Aristóteles definía como primera filosofía: el estudio del ser (aquello más general y común que comparten todas las entidades y cuyos rasgos son universales). Es una de las principales obras de la antigua filosofía griega y constituye una de las más influyentes de toda la historia de la filosofía occidental. Su título da nombre a una de las principales ramas filosóficas, la metafísica.

Sobre la polémica que ha desatado Hawking he leído una frase interesante, precisamente, de un teólogo:" La ciencia es atea y sería un milagro que pudiera probar la existencia o inexistencia de Dios".

Muy bueno

Fractales naturales y una reflexión informal

Reflexión informal sobre la fractalidad del mundo.

Fractal es un objeto matemático discontinuo, roto, fracturado. A primera vista, algo extraño, ajeno, que sin embargo impregna todo nuestro mundo. Lo que tocamos, lo que somos, por donde nos movemos... todo es fractal. Simplificamos la realidad para poderla entender, nos quedamos con la simplificación, sacamos su esencia y la convertimos en saber, pero la simple continuidad observada por doquier es una quimera.

Todo son simplificaciones. Si una línea real la ampliamos, veremos una inmensa cantidad de imperfecciones, de discontinuidades, que se incrementan según el aumento con que las observemos. Cualquier superficie lisa esconde multitud de cortes y hendiduras. Simplificamos y tratamos así de construirnos un mundo más sencillo, que no siempre está tan cerca de la realidad como creemos.

La continuidad de la materia ya se vio rota por el átomo, materia discreta que forma la materia "continua" que vemos y tocamos. Después se rompió la continuidad de la energía por obra y gracia del cuanto de acción ( h ) . La energía pasó a estar cuantificada, en “paquetes” de mayor o menor magnitud, según su mayor o menor frecuencia de vibración. La realidad pasó a ser granulada, como una película fotográfica. El cuanto de acción, que define el mínimo "grano de realidad", no permite un grano más fino y , a la vez , estable... Las consecuencias fueron terribles: el cuanto acabó con la nada, con el vacío, por pura incompatibilidad.


El vacío absoluto y estable suponía un grano infinitesimal, inexistente, suponía un cuanto de acción nulo, que no existe. El vacío absoluto y estable, la nada, desapareció y dejó en su lugar a un inmenso fractal llamado el espacio-tiempo.

Todo fractal esconde algo entre sus innumerables quebrados y vericuetos. ¿ Qué escondía la nueva nada? Escondía partes de ella misma, y dejó al descubierto la incertidumbre de Heisenberg, el mínimo "grano" de realidad.

Reedición de la entrada de La bella teoría de hace unos tres años.

+++ Teoría del caos (Instituto Astrofísico de Canarias)

El efecto mariposa, un atráctor extraño

El orden lleva asociado un grado importante de predicción, al caos le sucede lo contrario. Los sistemas lineales, representan el orden, son predecibles y cómodos de manejar, de ahí nuestra tendencia a generalizarlos. Ante un sinfín de situaciones generalizamos, proyectamos los datos del presente para tratar de averiguar un comportamiento futuro y casi siempre nos va bien. Pero existen sistemas que se resisten: pequeñas variaciones, incertidumbres, en los datos iniciales desembocan en situaciones finales totalmente descontroladas e impredecibles. Son los llamados sistemas caóticos (En la figura, atractor extraño "poisson_saturne" hecho con el programa Chaoscope).


Para estudiar estos sistemas se requiere de una metodología diferente. Su estudio se realiza en el llamado espacio de fases, un espacio abstracto en el que se representan todas las variables dinámicas del sistema. Por ejemplo, un péndulo simple ideal se vería representado por dos variables, la velocidad y la posición de la masa suspendida. Su representación podría hacerse, por tanto, en el plano y sería una circunferencia. Cada punto de la misma representaría dos cantidades, la velocidad y la posición, en ese momento.


Esa figura en el espacio de fases, a la que se aproxima el fenómeno estudiado, se le llama su atractor. En los sistemas no caóticos el atractor suele ser un punto, una circunferencia, una figura geométrica conocida, pero en los sistemas caóticos presenta una forma “extraña”, de ahí que reciba el nombre de “atractor extraño”, con una dimensión fraccionaria o fractal (En la figura, atractor de Lorenz, en 3D, con el programa Chaoscope).

El primero de éstos fue hallado, por casualidad, por el meteorólogo Edward Lorenz cuando trataba de encontrar un modelo matemático que permitiera predecir el comportamiento de grandes masas de aire. Consiguió ajustar el modelo a sólo tres variables que indican como cambian la velocidad y la temperatura del aire a lo largo del tiempo (atractor de Lorenz).


Después de haber estudiado el modelo, volvió a introducir los datos iniciales - esta vez con menos decimales- y el resultado que obtuvo fue completamente diferente del anterior. Cuando reflexionó sobre los resultados se dio cuenta que el sistema era extremadamente sensible a las condiciones iniciales: pequeñas perturbaciones en los datos de partida tienen una gran influencia sobre el resultado final. Sus ecuaciones captaban la esencia de la verdadera atmósfera. “Aquel primer día ( invierno de 1961) decidió que los pronósticos amplios estaban condenados a la extinción”. Pero vio más que azar en su modelo del tiempo: una fina estructura geométrica, orden disfrazado de casualidad.


Para explicar de una manera gráfica – y exagerada - la cuestión se le ocurrió que el simple aleteo de una mariposa, que no se hubiera tenido en cuenta en los datos iniciales, podía modificar una predicción hasta hacerla totalmente inviable después de un determinado tiempo.


Sobre el efecto mariposa se han escrito cientos de artículos, novelas, canciones y se han hecho películas. En un artículo de Enrique Dans, profesor del Instituto de Empresa, se compara el “ecosistema de Internet” con los sistemas no lineales y complejos como el tiempo atmosférico:” Las variables en juego (en Internet) no son tantas: si en el clima hablamos fundamentalmente de velocidad y temperatura del aire, en Internet hablamos de visitas, vínculos y cuestiones afines. Pero el posible impacto de una variación infinitesimal en medición de las variables de origen puede tener un impacto brutal en los resultados finales,...” . “ Criterios que todo el mundo, aparentemente, da por buenos, como el sacrosanto PageRank de Google, la cuenta de vínculos entrantes de una página web que lleva a cabo Technorati o los rankings de popularidad de Alexa son medidas completamente burdas, groseras, carentes de inteligencia, que responden únicamente al deseo e intentar reducir la incertidumbre, pero que lo hacen, en general, bastante mal.”


En este sentido nos encontramos en la era anterior al descubrimiento del efecto mariposa, utilizamos métodos lineales para tratar de analizar los sistemas complejos, no lineales, en donde las realimentaciones de todo tipo, y a todos los niveles, son la propia esencia del sistema. Necesitamos conocer "el atractor extraño de Internet".

Para saber más:"Caos,La creación de una ciencia", de James Gleik. Seix Barral. Barcelona 1988. Un magnífico libro.

Nueva edición del post del mismo título de fecha 17/10/2006. Un saludo y feliz verano amigos.

La información, el azar y el número Pi

La información se nos presenta como una entidad fundamental, no sólo a nivel de la estructura física de la materia (entropía) sino de la propia estructura de los números trascendentes, tales como Pi , y también del resto de los números irracionales, que constan de infinitos decimales dispuestos de forma aleatoria, como por ejemplo la raíz cuadrada de 2. El azar que encontramos en infinidad de procesos naturales, o en los números, es extraordinariamente difícil de simular de forma artificial, lleva asociado un nivel de información neutro (cero información añadida), que en cierta forma es una restricción poderosa y de gran calado.

El número Pi es, junto con el número e, uno de los números llamados trascendentes más famoso. Es la relación entre la longitud de la circunferencia y su diámetro, y aparece en infinidad de expresiones matemáticas o físicas. Desde la antiguedad, muchas veces por cuestiones prácticas, se ha tratado de calcular el mayor número de decimales para conseguir más precisión en las medidas (en la figura, Arquímedes de Siracusa - 250 a.C - lo calculó con la aproximación: entre 3+10/71 y 3+1/7). Casi a semejanza de los alquimistas que trataban de conseguir la piedra filosofal, los geómetras de todos los tiempos han tratado de hallar la cuadratura del círculo. Actualmente gracias a la potencia de cálculo de nuestros ordenadores se han conseguido millones de sus decimales. Teóricamente tiene infinitos decimales y deben estar situados de forma completamente aleatoria, de manera que al cabo de miles de millones de trillones de decimales que busquemos podremos encontrar cualquier combinación, que convenientemente codificada podría contener: El Quijote, Romeo y Julieta, la Biblia o este propio escrito.

Existen varias páginas que encuentran cualquier combinación de números entre las cifras de Pi, y nos dicen a partir de qué decimal se puede encontrar. Al reflexionar sobre ello, pensé que se podría codificar, de forma ventajosa, cualquier información sobre esta base y me puse manos a la obra. Busqué la posición de una codificación al azar, el número 11, y la encontré a partir del decimal 94. El número 111 a partir del decimal 153 y así hasta el 11111111 que se encuentra a partir de la posición 159 090 113, en la ristra de decimales del número Pi. Pronto me di cuenta de que no significaba ninguna simplificación pues para dar la posición dentro de Pi de un determinado código, se necesitarían, en general, un número de dígitos igual o superior a la propia codificación que se busca. Repetí la búsqueda para la codificación 121212 que se encuentra a partir de la posición 241 987 (seis dígitos para definir la búsqueda del código 121212) : 3,14 .......28979301308065657163 121212 07914290705421508889........ En base a esta suposición el Quijote se encontraría codificado, en los dígitos del número Pi, alrededor del decimal 4x10^1000000 (un 4 seguido de un millón de ceros), más o menos.

En cierta forma, podríamos decir que la información mínima ni se crea ni se destruye, simplemente se transforma. El azar no debe llevar implícitamente ninguna información que pueda después utilizarse y esto lo encontramos en infinidad de procesos naturales, o en los números. Supongo que debe ser así, pues no sería lógico que pudiésemos codificar El quijote, por dar un código como ejemplo, con otro código mucho menor, irrazonablemente menor. Si codificamos y comprimimos ese código, la forma de indicar su posición dentro de Pi deberá contener una información similar. Al menos eso es lo lógico, y en base a esa lógica de cero información añadida, o información neutra, deben estar distribuidos al azar los dígitos de Pi y de los innumerables números irracionales con infinitos dígitos.

Segunda edición del post de fecha 22/02/2007. Un saludo amigos.

Libertad cuántica

Hola amigos, en un tiempo en que una serie de pueblos, tradicionalmente oprimidos, tratan de despojarse de viejos sistemas autocráticos y despertar a la libertad, las partículas más elementales que forman toda la materia de nuestro universo nos dan una lección de su caracter indomable. La libertad, en cierta forma, está impresa más allá de nuestros genes en la esencia de la propia materia. Paso a reeditaros un antiguo post que habla de la "libertad cuántica". Un abrazo.



Las partículas elementales parecen poseer una cierta "libertad cuántica". Para ellas los sucesos no están estrictamente determinados, como lo fueron para las partículas en la física clásica del siglo XIX, y poseen un elemento de elección dentro de ciertos límites, siempre que en promedio obedecezcan las leyes clásicas. El cuanto de acción, h, les da esa libertad.

Tratemos de confinar un electrón dentro de un núcleo atómico. Después de todo ¿por qué no deben los electrones ser un componente de los núcleos como los protones y los neutrones? Los neutrones experimentan una desintegración radiactiva que los convierte en un protón y un electrón (radiación beta). Por tanto, un electrón atrapado por un protón para formar un neutrón parecería una idea razonable, pero el electrón rehúsa cooperar, se niega a ser confinado.

Un electrón confinado a un espacio de dimensiones nucleares debe tener longitudes de onda asociadas a él tan cortas, al menos, como el diámetro del núcleo. Si las ondas fueran mayores significaría que el electrón consume la mayor parte de su tiempo fuera del núcleo, y eso no funcionaría. Sin embargo, las longitudes de onda cortas implican una restricción en espacio, y ello debe estar equilibrado por un incremento del momento con objeto de conservar su cuanto de acción fundamental, h ( (incremento de espacio) x (incremento de momento) = cuanto de acción (h)) . El electrón tendría tanta energía cinética que saldría de su jaula nuclear. El encarcelamiento no puede realizarse. Los electrones no pueden existir dentro del núcleo en un estado estable, a menos que se ejerza una tremenda fuerza para vencer su empuje hacia la libertad.

Sólo una fuerza tan inmensa como la presión de una estrella que se desintegra bajo su propia gravedad puede apiñar electrones en núcleos para formar un cuerpo compuesto completamente por neutrones: la estrella de neutrones. Y ello es una medida gráfica de lo fuerte que es la urgencia de libertad del electrón. Necesita que un cuerpo del tamaño de una estrella se siente sobre él.

Cada vez que tratamos de restringir la libertad cuántica de un electrón, ya sea forzándolo a entrar en algún espacio o dirigiéndolo a través de hendiduras, éste insiste en su libertad de acción y la manifiesta de una forma característica, y no sólo de forma pasiva. Puede promover su libertad violando las leyes (clásicas) de la conservación de la energía y el momento.


Del estupendo librito " Tiempo, espacio y cosas", de B.K. Ridley, título original "Time, space and things", publicado por Cambridge University Press. Traducción de 1989 del Fondo de Cultura Económica. Pura belleza al servicio de la divulgación científica.

Reciente teoría:

Puede que el comportamiento de las partículas cuánticas no sea tan extraño. Según una reciente teoría que conjuga nuestro conocimiento sobre fractales y agujeros negros, las partículas podrían ser comparadas con una serie de trenes moviéndose sobre una intrincada red fractal de vías. La aparente libertad que observamos en su movimiento se ciñe a ese entramado de vías que desconocemos. No podemos forzar cualquier movimiento arbitrario que permita que el “tren se salga de la vía”.
Ese entramado de vías se correspondería con el llamado conjunto invariante del universo, un mínimo de información subyacente que engloba el número total de estados posibles en el mismo. La supuesta libertad del electrón se ceñiría a seguir ese conjunto mínimo de información que determina, aunque no lo veamos, sus movimientos. (Fuente: Ciencia Kanija)