Una fórmula maravillosa

Desde que la vi no la he podido olvidar... Relaciona los números imaginarios ( i = raíz cuadrada de ( –1)), con las potencias ( número e y logaritmos neperianos ) y con las funciones trigonométricas. Me ha permitido recordar, sin esfuerzo, fórmulas trigonométricas como la del seno o coseno de una suma de ángulos, del ángulo doble o mitad, y calcular, con facilidad, derivadas de funciones trigonométricas.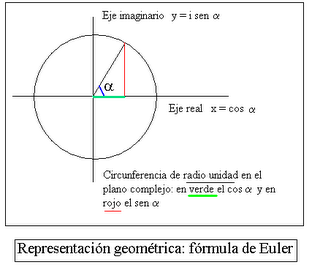
Nos la podemos encontrar en cualquier sitio, en cualquier expresión matemática pura o relacionada con algo tan prosaico como las relaciones de impedancias en un circuito de corriente alterna. En la función de onda de la mecánica cuántica o en cualquier expresión de naturaleza ondulatoria o periódica. En la técnica, en la física o en las matemáticas más abstractas ( Roger Penrose reflexiona– en su último libro,en el capítulo sobre las diferenciales complejas - lo que habría disfrutado Euler con todas las maravillas de su fórmula y de los números imaginarios ).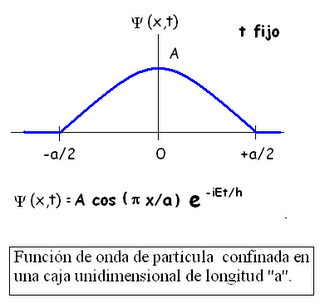
La fórmula de Euler fué demostrada por primera vez por Roger Cotes en 1714, y luego redescubierta y popularizada por Euler en 1748. Es interesante notar que ninguno de los descubridores vió la interpretación geométrica ( circunferencia en el plano complejo): la visión de los números complejos como puntos en el plano surgió unos 50 años mas tarde con Caspar Wessel, y d'Argaud.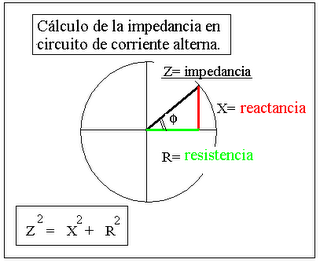
En la figura, para el cálculo de la impedancia, el eje imaginario representa la reactancia, resultado de la resta entre la parte inductiva ( bobinas ) y la parte capacitiva ( condensadores). El ángulo ( phi ) que forman la impedancia con el eje real de la resistencia pura es sumamente importante en la industria, su coseno es lo que llamamos el factor de potencia que mide, en cierto modo, la eficiencia de un circuito. Para un ángulo grande la reactancia asociada es grande y obliga a las compañías eléctricas a suministrar una potencia reactiva adicional y a la industria a pagar un consumo innecesario. Este ángulo se corrige añadiendo baterías de condensadores que ofrecen una reactancia de signo contrario a la presentada por los motores industriales.
Lo tiene todo, es sencilla, bonita, elegante y útil, muy útil. Sin duda es una fórmula maravillosa.












11 comentarios:
todo es oes muy cierto, pero cómo fue que se le ocurrio a Euler?, hay una teoría que dice que era tan genial que solo la escribio por que calzaba a la perfección, además no hay ni un indicio que diga que estaba escribiendo Euler para que se le ocurriera semejante belleza fue algo instintivo,
Seria bueno averiguar más sobre la ecuación más bella,
Saludos
Pues si que es una formula bella, cuando la vi por primera vez en un curso elemental de variable compleja, nos la dieron muy a la ligera, pero el resto de la clase no pude dejar de pensar que relacionaba esos numeros tan importantes, es como si las matematicas tuvieran inteligencia propia
bella y útil, desde luego, pero el cálculo complejo no lo entiende (ni se lo cree) nadie
Anónimo: tienes razón. La culpa es de la pésima enseñanza. Casi nadie la entiende (yo tampoco). Hazte, sin embargo, esta pregunta clave: ¿Cuál es la diferencia entre una función de variable compleja y una de dos variables reales? La respuesta es que las dos partes (R e I) de la variable compleja se comportan "solidariamente". Esa "solidaridad" es lo que establecen las ecuaciones de Cauchy-Riemann. Así que éstas ecuaciones NO son una propiedad de la funciones de variable compleja -como suelen enseñarse- sino más bien su definición. Creo que esta pista es clave. Suerte. (anónimo 2)
personalmente me parece mas bella la forma que adopta la formula de euler cuando se hace alpha = pi, de forma que queda:
exp{i*pi} + 1 = 0, ecuacion que vincula los numeros e, i, pi, 1 y 0.
Para el primer anónimo que dejó un mensaje: que uno no entienda algo, no significa que nadie lo entienda. Si tu no entiendes los números complejos, probablemente te falten muchas horas de dedicación. Yo tampoco entiendo muchas cosas de variable compleja, pero sé que es debido a mi falta de trabajo en ese campo. Aplícate el cuento, y estudia, Cuando entiendas algo, podrás criticarlo (y, esperemos, mejorarlo!). Eso es ciencia.
Para Anónimo 1: que tu no lo entiendas, no significa que nadie lo entienda. En cuanto a "creer" el cálculo complejo, se te olvida que esto es ciencia, no hay que creer ni tener fe. Hay que comprobar. Y hasta el momento, el cálculo complejo es correcto, la cuántica se basa en los números complejos, y todo se ajusta a los experimentos. No es cuestión de creer, es cuestion de estudiar, echarle horas delante de los libros, y cuando uno lo entienda, podrá pensar si es correcto, o no. Así que. ánimo y a empollar. Cuéntanos lo que descubras.
entiendo que i*i= -1, y haciendo divertidos arreglos con algunas expansiones en series, u otro método por allí , se llega a esa ecuación ...yo lo veo como idolatrar a alguien que no lo merece..........en todo caso me conmueve mas la primera expresión.......por ser la precursora de las posteriores álgebras que nacieron después de aquella
todo es verdad creo, pero quien es el verdadero creador de la ecuacion de cauchy-riemann
Desde un punto de vista histórico fueron tratadas ya en el siglo XVIII por D’Alembert. Euler las desarrolló en sus trabajos de
aplicación a la mecánica de fluidos, a la cartografía y al cálculo integral.
Son llamadas Ecuaciones de Cauchy-Riemann, aunque, realmente habrían de llamarse, más apropiadamente, Ecuaciones de D’Alembert-Euler.
Un saludo.
Me parece ,que, mejor pongance a estudiar matematicas, no hay nada de maravillo.
La naturaleza , el universo, Todo por si mismo son matematicas.
Publicar un comentario