Simetría de grupo: relatividad especial,invarianza, leyes de conservación, clasificación de las partículas elementales...

Cuando estudiaba en el instituto la teoría de grupos no tenía ni idea para que servía todo aquello, pero las representaciones de los elementos, componiéndose unos con otros mediante las diferentes operaciones que se definían, mostraban un orden sorprendente. Me habría impresionado saber que esas simetrías que presentaban y su belleza simple, puramente matemática, representa a la perfección la simetría del espaciotiempo y de las partículas subatómicas de las que estamos formados. La utilidad, aparte de la belleza, siempre es un aliciente añadido, la naturaleza suele “confundir” la una con la otra: la solución más útil y eficaz suele ser, además, la más bella. La teoría de grupos es por su sencillez, potencia y armonía una verdadera teoría NATURAL.

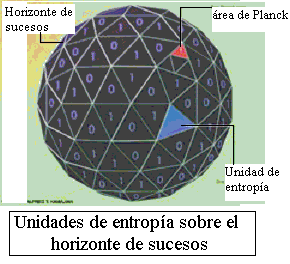
De forma muy simple, se habla de que existe simetría cuando se realiza una operación sobre algún objeto y este permanece invariante ( invarianza). Una esfera tiene simetría de forma ante un giro o ante un desplazamiento, es decir, sigue conservando su aspecto ante estas operaciones de simetría. Este tipo de simetrías continuas ( independiente de la magnitud del ángulo girado, o de la cantidad de la variable considerada) se encuentran, fácilmente, en la naturaleza y de ellas se desprenden leyes tan fundamentales como la conservación de la energía, tal como demostró en un importante teorema la eminente matemática Emmy Noether, a principios del siglo XX ( simetrías contínuas <--> leyes de conservación).
La idea básica de la aplicación de la teoría de grupos al mundo físico es describir, simbólicamente, estas operaciones de simetría utilizando el álgebra. Si una rotación sobre un eje 1 con un determinado ángulo la llamamos R1, R2 y R3 serán otras dos rotaciones diferentes sobre ejes llamados 2 y 3 con distintos ángulos. El producto R2xR1 se entenderá como la aplicación del giro R1 y después del giro R2. Este producto tiene tres propiedades simples pero muy importantes que se encuentran en la base de la bella teoría de grupo: asociativa [ R1x(R2xR3) = (R1xR2)xR3], existencia de identidad o elemento neutro ( rotación nula) y de inverso o elemento simétrico ( dos rotaciones dejan el objeto como la rotación nula). De estos tres simples axiomas brota la bella estructura de la teoría matemática de grupo.

Las propias leyes de transformación espaciotemporal de Einstein ( teoría de la relatividad restringida) son una generalización de las transformaciones del espacio de tres dimensiones al espacio de tres dimensiones espaciales más el tiempo ( espaciotiempo de Minkowski). Eugene Wigner, en 1939 escribió un artículo demostrando que cuando se aplicaba la condición algebraica de grupo de simetría a una descripción matemática del mundo, automáticamente se presuponía que se cumplirían los principios de relatividad especial y, además, las partículas elementales podían clasificarse con sencillez.


Las partículas se podían clasificar por el valor de su masa en reposo ( fuese o no cero) y por una propiedad, puramente cuántica, su espín – una especie de rotación intrínseca- cuyo valor en unidades especiales referenciadas a la constante de Plank, sólo puede ser de valor entero 0,1,2,3 ... o fraccionario 1 /2 , 3/2, 5/2, etc.
Las partículas con espín entero son llamadas bosones y las de espín fraccionado fermiones. Esta clasificación es de gran importancia porque según la clase de giro o espín que presenten las partículas sus reacciones son completamente diferentes.Los bosones son partículas de “fuerza” y los fermiones de “materia”, los primeros pueden ocupar el mismo estado cuántico y para los segundos eso es imposible .

De tres simples axiomas brota la bella estructura de la teoría matemática de grupo.


FIGURAS.- Primera: Representación de un grupo sencillo de cuatro elementos con leyes de composición interna (+) y (x), llamadas así porque al aplicarlas a sus elementos el resultado sigue perteneciendo al grupo ( "i" es la ráiz cuadrada de -1).Este grupo por ser conmutativo ( AxB =BxA), se llama abeliano o conmutativo. El elemento neutro del grupo es el +1, y el simétrico de -1 es -1, el de i es -i, etc.Segunda: El matemático N. Abel , genial introductor de la teoría de grupos, de trágica y temprana muerte a los 26 años. Tercera: Ilustración sobre Einstein/ teoría relatividad especial. Cuarta: Representación bosón-fermión.

Para saber más : Excelente artículo de Astrocosmo.

Enamorarse de la ciencia

Recientemente, ha estado en España Gerald Holton, profesor de física e historiador de la ciencia en Harvard, un verdadero especialista en Einstein, hasta tal punto que fue la persona elegida por la familia del científico para clasificar toda su documentación, después de su muerte. En la entrada de 18/6/06 , Ciencia/tecnología e imaginación, resumí una entrevista suya a la revista Mètode de la Universidad de Valencia.


En su última visita ha concedido una entrevista al periódico el El País. Le preguntaron, cuál es la característica esencial de un científico y Holton respondió: "Tal vez mis colegas sonrían, pero creo que igual que algunas personas están enamoradas del dinero y otras se enamoran del arte -ayer estuve en uno de sus maravillosos museos: el Prado, y es extraordinario-, los científicos están enamorados de la química o de la física o de las matemáticas... El científico se enamora muy joven y deja todo de lado por ese amor. Stephen Jay Gould decía que la ciencia significa que al final del día, en el laboratorio, sabes que el 99% del tiempo de trabajo ha sido tiempo perdido, y encima todavía tienes que limpiar las jaulas de los ratones. La ciencia es una actividad que exige muchísima dedicación y tiempo".

En el periódico, el titular de la entrevista decía :” Los científicos están enamorados de la química, de la física o de las matemáticas...”. Poco después, cuando he comprado el último y monumental libro de Roger Penrose “ El camino a la realidad ”, una guía completa de las leyes del universo, me ha llamado, poderosamente la atención la dedicatoria del mismo a su querido profesor Dennis Sciama (también profesor de Stephen Hawking) : ”A Dennis Sciama, que me mostró la emoción de la física”.


Hace muy poco, he vuelto a releer el formidable ensayo de Isaac Asimov “ El electrón es zurdo”. Al comienzo del mismo dice, entre broma y serio:”Por un lado, mi objeto y mi pasión, aun en mis novelas, es explicar. En parte es por instinto misionero por lo que anhelo conseguir que mis lectores vean y entiendan el Universo, como yo lo veo y entiendo, para que puedan gozarlo como yo.”

Amor, emoción, gozo por la ciencia.

Y en muchas ocasiones hace falta verdadero amor. Por ejemplo, para seguir en España en el puesto de científico becario hasta los 40 años, después de grandes esfuerzos y una gran y costosa preparación. Recientemente, Francisco Tomás, rector de la Universidad de Valencia hacía unos comentarios interesantes, a la revista Mètode de la Universidad ( número 50 ), sobre el estado actual de la ciencia:” En estos momentos hay una regresión a escala mundial del interés de los jóvenes por cursar carreras científicas, es un hecho muy inquietante”... “ Existe una intensa dedicación de los investigadores en producir conocimiento, pero esta producción ha dejado muy al margen la necesidad de difundirlo en la sociedad: el hecho de realizar una investigación competitiva, publicando en revistas de alta exigencia, ha dejado paradójicamente un poco de lado la divulgación de nuestro trabajo. Se ha producido un desfase, hay muy pocos comunicadores de la ciencia y también hay muy pocos científicos que tengan ese interés por la difusión...”

Y eso, la divulgación, es esencial para crear el tejido social necesario para que exista una “cantera” de futuros científicos. Sólo se consigue esa “cantera” transmitiendo la emoción por la ciencia, como decía Roger Penrose, y desde luego, creando las condiciones dignas para ejercerla. Hacen falta las dos cosas.

¿Universo holográfico?

Los resultados teóricos relativos a la entropía de los agujeros negros llevan a concluir que el universo podría ser un inmenso holograma. Jacob D. Bekenstein.

Del estudio de las propiedades de los agujeros negros se han deducido los límites absolutos que acotan la información que cabe en una región del espacio. Teniendo en cuenta que esos límites dependen de la materia y energía contenida en ese espacio es asombroso que se pueda deducir un límite sin conocer ni siquiera , con absoluta certeza, el último componente de la materia ( se cree que los quarks y los electrones son excitaciones de supercuerdas que deben ser los entes fundamentales, pero no se descartan niveles más bajos).

La clave está en la entropía, en 1877 , Ludwing Boltzmann la caracterizó como el número de estados microscópicos distintos ( N) en los que pueden hallarse las partículas que componen un trozo de materia de forma que siga pareciendo el mismo trozo desde un punto de vista macroscópico.

Las dos entropías: Cuando el matemático Claude E. Shannon buscó una manera de cuantificar la información contenida en un mensaje, la lógica le llevó a una fórmula que tenía el mismo aspecto que la de Boltzmann. Después se vio que la entropía termodinámica y la de Shannon son conceptualmente equivalentes: el número de configuraciones que se cuentan en la entropía de Boltzmann refleja la cantidad de información de Sannon que se necesitaría para realizar cualquier configuración determinada.

Se pensaba que cuando caía la materia en un agujero negro desaparecía también con ella su entropía, pero Demetrious Christodoulou ( 1970) y Stephen W. Hawking demostraron que en el proceso de fusión de dos agujeros negros, nunca decrecía el área total de los horizontes de sucesos. A partir de estos estudios y del posterior descubrimiento de que los agujeros negros emiten radiación , precisamente llamada radiación de Hawking ( 1974) ser su descubridor, se determinó la constante de proporcionalidad entre la entropía de un agujero negro y el área del horizonte: La entropía del agujero negro es exactamente una cuarta parte del área del horizonte de sucesos medida en áreas de Plank ( 10 ^–66 centímetros cuadrados). Es como si la entropía, en cuanto medida de información, estuviese escrita sobre el horizonte de sucesos, de suerte que cada bit ( cada 0 ó 1 de la codificación digital) correspondiera a 4 áreas de Planck.

Este sorprendente resultado tiene una explicación natural si es cierto el principio holográfico propuesto en 1993 por el Premio Nobel Gerard `t Hooft, de la Universidad de Utrech, y elaborado por Leonard Susskind. Sobre esta teoría, Juan Maldacena, de la Universidad de Harvard, en un reciente artículo de enero del 2006, en Investigación y Ciencia, afirma que: “ La fuerza de la gravedad y una de las dimensiones espaciales quizá procedan de las peculiares interacciones, entre partículas y campos, existentes en un espacio con menos dimensiones”.



La descripción tridimensional con ley de gravedad sería equivalente a la descripción holográfica sin gravedad y en dos dimensiones, de modo que un determinado cálculo demasiado difícil en una descripción puede resultar trivial en la otra. A pesar de su radical diferencia, las dos teorías describirían por igual todo lo que vemos y cualquier dato que pudiésemos recoger sobre el funcionamiento del universo.


Un holograma es un objeto bidimensional que codifica toda la información que describe la imagen tridimensional. Nuestro Universo tridimensional podría estar codificado en una superficie que lo contiene, como una especie de inmenso holograma. Los experimentos de física de partículas de altas energías, según Juan Maldacena, quizás hayan encontrado ya indicios de la validez de este principio.


Nota final: En el post sobre los condensados de Bose–Einstein, me llamó la atención un artículo del Dr. Fernando Sols de la Universidad Complutense. En él hablaba de separar un condensado de varios millones de átomos en dos partes tratando de que siguieran estando en coherencia cuántica. Le comenté, por correo, que con este tipo de “superátomos” que son los condensados de B-E se podría hacer un experimento sobre el principio holográfico. Me contestó muy amablemente, aclarándome las dificultades que entrañaría mantener la coherencia de las dos partes del condensado. Si se consigue la coherencia entre las dos partes del condensado, nos encontraríamos con la paradoja de que en cada parte del condensado no tendremos la mitad de los átomos, sino que todos los átomos estarían a la vez en las dos partes. Aunque difícil, esta podría ser una vía interesante de constatación del principio holográfico.

Investigación y cienca. Octubre-2003 y enero-2006.

Una fórmula maravillosa

Desde que la vi no la he podido olvidar... Relaciona los números imaginarios ( i = raíz cuadrada de ( –1)), con las potencias ( número e y logaritmos neperianos ) y con las funciones trigonométricas. Me ha permitido recordar, sin esfuerzo, fórmulas trigonométricas como la del seno o coseno de una suma de ángulos, del ángulo doble o mitad, y calcular, con facilidad, derivadas de funciones trigonométricas.


Nos la podemos encontrar en cualquier sitio, en cualquier expresión matemática pura o relacionada con algo tan prosaico como las relaciones de impedancias en un circuito de corriente alterna. En la función de onda de la mecánica cuántica o en cualquier expresión de naturaleza ondulatoria o periódica. En la técnica, en la física o en las matemáticas más abstractas ( Roger Penrose reflexiona– en su último libro,en el capítulo sobre las diferenciales complejas - lo que habría disfrutado Euler con todas las maravillas de su fórmula y de los números imaginarios ).

La fórmula de Euler fué demostrada por primera vez por Roger Cotes en 1714, y luego redescubierta y popularizada por Euler en 1748. Es interesante notar que ninguno de los descubridores vió la interpretación geométrica ( circunferencia en el plano complejo): la visión de los números complejos como puntos en el plano surgió unos 50 años mas tarde con Caspar Wessel, y d'Argaud.

En la figura, para el cálculo de la impedancia, el eje imaginario representa la reactancia, resultado de la resta entre la parte inductiva ( bobinas ) y la parte capacitiva ( condensadores). El ángulo ( phi ) que forman la impedancia con el eje real de la resistencia pura es sumamente importante en la industria, su coseno es lo que llamamos el factor de potencia que mide, en cierto modo, la eficiencia de un circuito. Para un ángulo grande la reactancia asociada es grande y obliga a las compañías eléctricas a suministrar una potencia reactiva adicional y a la industria a pagar un consumo innecesario. Este ángulo se corrige añadiendo baterías de condensadores que ofrecen una reactancia de signo contrario a la presentada por los motores industriales.

Lo tiene todo, es sencilla, bonita, elegante y útil, muy útil. Sin duda es una fórmula maravillosa.

Polvo fractal con dimensión entera

Como comentaba en el post sobre el “Vacío cuántico, vacío fractal ”, la existencia del cuanto de acción ha destruido por completo la propia noción de trayectoria clásica.
Laurent Nóttale complementó la definición de Richard Feynman (1965) y A. Hibbs sobre las trayectorias virtuales típicas de una partícula cuántica, indicando que los caminos cuánticos posibles son, en número infinitos, y todos son curvas fractales caracterizadas por una propiedad geométrica común: su dimensión fractal es 2.

En algunos foros he leído que no se entendía bien lo de la dimensión fractal entera, en este caso 2, pero tal como indicaba en la expresión general de la dimensión fractal:

Dimensión fractal = dimensión topológica + factor dimensional

( El factor dimensional, siempre positivo, es tanto mayor cuanto más irregular es el fractal: indica la capacidad de ocupar más espacio del que indica su propia dimensión topológica)

Si el factor dimensional es entero, también lo será la dimensión fractal. Eso es lo que ocurre con las trayectorias virtuales en mecánica cuántica y también en una serie de fractales típicos, como puede ser el fractal del movimiento browniano en un plano ( dimensión fractal 2) o la curva de Peano ( dimensión fractal 2) que tiene más de 100 años de existencia.


Si una curva clásica tiene dimensión topológica 1, cuando hablamos de curvas fractales con una dimensión entre 1 y 2 estamos indicando que son capaces de ocupar parte del plano. Y es precisamente esa capacidad la que viene expresada por el factor dimensional. En el caso de la curva de Peano o del movimiento browniano, en el límite, ocupan todo el plano, de ahí que su dimensión fractal sea 2 , la propia dimensión del plano.


Como ejemplo, todavía más llamativo, observamos en la figura un fractal clásico ( el primero que se conoce), el polvo de Cantor que toma toma su nombre de Georg Cantor que en 1883 lo utilizó como herramienta de investigación para una de sus principales preocupaciones: el continuo.






A partir de una recta se le van quitando los segmentos centrales hasta conseguir una serie infinita de puntos aislados, de ahí el nombre de polvo. Si restablecemos de forma escalonada el segmento que antes le quitábamos, el nuevo fractal sigue teniendo estructura quebrada y autosemejante , pero ahora en lugar de tener una dimensión fractal igual a log 2/ log 3 tiene una dimensión entera: log 3/ log 3 =1. Nos ayuda, también, a entender como se calcula, de forma práctica, la dimensión fractal de una figura.


Esta otra figura es una síntesis de dos de los fractales clásicos, Koch y Cantor, y nos ayuda de forma intuitiva a entender el cálculo de su dimensión fractal. En la figura original de Koch, sobre los segmento A1-B1-D1-E1 se construye la figura que forman los segmentosA-B-C-D-E. Su dimensión fractal es log 4/ log 3 ( cuatro segmentos sobre tres). En la nueva construcción se ha sustraido 1/4 de cada uno de los segmentos superiores para dejar 4 segmentos de longitud 3/4: al final son 3 sobre 3 ( log 3/ log 3 = 1).

Se pueden construir infinidad de fractales con dimensión entera y, precisamente, esa irregularidad que representa una dimensión fractal entera en un fractal creo que nos ayuda a entendelos mejor.