Polvo fractal con dimensión entera

Como comentaba en el post sobre el “Vacío cuántico, vacío fractal ”,  la existencia del cuanto de acción ha destruido por completo la propia noción de trayectoria clásica.

Laurent Nóttale complementó la definición de Richard Feynman (1965) y A. Hibbs sobre las trayectorias virtuales típicas de una partícula cuántica, indicando que los caminos cuánticos posibles son, en número infinitos, y todos son curvas fractales caracterizadas por una propiedad geométrica común: su dimensión fractal es 2.

En algunos foros he leído que no se entendía bien lo de la dimensión fractal entera, en este caso 2, pero tal como indicaba en la expresión general de la dimensión fractal:

Dimensión fractal = dimensión topológica + factor dimensional


( El factor dimensional, siempre positivo, es tanto mayor cuanto más irregular es el fractal: indica la capacidad de ocupar más espacio del que indica su propia dimensión topológica)

Si el factor dimensional es entero, también lo será la dimensión fractal. Eso es lo que ocurre con las trayectorias virtuales en mecánica cuántica y también en una serie de fractales típicos, como puede ser el fractal del movimiento browniano en un plano (dimensión fractal 2)  o la curva de Peano (dimensión fractal 2) que tiene más de 100 años de existencia.


Si una curva clásica tiene dimensión topológica 1, cuando hablamos de curvas fractales con una dimensión  entre 1 y 2 estamos indicando que son capaces de ocupar parte del plano. Y es precisamente esa capacidad la que viene expresada por el factor dimensional.  En el caso de la curva de Peano o del movimiento browniano, en el límite, ocupan todo el plano, de ahí que su dimensión fractal sea 2 , la propia dimensión del plano.



Como ejemplo, todavía más llamativo, observamos en la figura un fractal clásico
 (el primero que se conoce), el polvo de Cantor que toma toma su nombre de Georg  Cantor  que en 1883 lo utilizó como herramienta de investigación para una de sus principales preocupaciones: el continuo.





A partir de una recta se le van quitando los segmentos centrales hasta conseguir una serie infinita de puntos aislados, de ahí el nombre de polvo. Si restablecemos de forma escalonada  el segmento que antes le quitábamos, el nuevo fractal sigue  teniendo estructura quebrada y autosemejante , pero ahora en lugar de tener una dimensión fractal igual a log 2/ log 3 tiene una dimensión entera: log 3/ log 3 =1. Nos ayuda, también,  a entender como se calcula, de forma práctica, la dimensión fractal de una figura.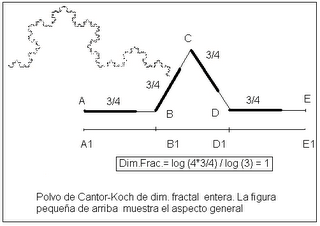



Esta otra figura es una síntesis de dos de los fractales clásicos, Koch  y  Cantor, y nos ayuda de forma intuitiva a entender el cálculo de su dimensión fractal. En la figura original de Koch, sobre los segmento A1-B1-D1-E1 se construye  la figura que forman los segmentosA-B-C-D-E. Su dimensión fractal es  log 4/ log 3  ( cuatro segmentos sobre tres). En la nueva construcción se ha sustraido 1/4 de cada uno de los segmentos superiores para dejar 4 segmentos de longitud 3/4: al final son 3 sobre 3 (log 3/ log 3 = 1).

Se pueden construir infinidad de fractales con dimensión entera y, precisamente, esa irregularidad que representa una dimensión fractal entera en un fractal creo que nos ayuda a entendelos mejor.

NOTA: Este post se publicó también en la revista Ciencia Abierta de la Universidad de Chile, en el número 31, sección de Educación, artículo nº 14 de dicha sección. Allí se añadió una parte más sobre la llamada dimensión de Hausdorff-Besicovitch:


En 1975 Benoit Mandelbrot publicó un ensayo titulado” Los objetos fractales: forma, azar y dimensión”. En la introducción comentaba los conceptos de objeto fractal y fractal como términos que había inventado a partir del adjetivo latino “fractus” ( roto, fracturado). Posteriormente, en 1982, publicó el libro “The Fractal Geometry of Nature”, en donde proponía : “Un fractal es, por definición, un conjunto cuya dimensión de Hausdorff-Besicovitch es estrictamente mayor que su dimensión topológica.”

De forma simplificada, esa dimensión tan rara se podría entender de la siguiente manera: Una línea recta de longitud N queda recubierta por un número N de segmentos de longitud unidad. Podemos expresarlo diciendo que longitud_línea = N⁽⁺¹⁾. Un cuadrado con lado N queda recubierto por N² pequeños cuadrados de lado la unidad. De forma similar a la línea se puede expresar que superficie_cuadrado = (N)⁽⁺²⁾. Sabemos que una línea recta tiene dimensión topológica 1 y una superficie dimensión 2. Para
recubrirlos necesitamos un elemento similar pero más pequeño N^D veces (en estos ejemplos de magnitud unidad). En general, el exponente D , generalizado a cualquier objeto, representa la dimensión de Hausdorff-Besicovitch del objeto.

Han sido propuestas otras definiciones y, de hecho, estamos ante un concepto geométrico para el que aún no existe un una definición precisa, ni una teoría única y comúnmente aceptada.

Kenneth Falconer, en su obra titulada “Fractal Geometry: Mathematical Foundations and Applications”, en 1990, describe un concepto de estructura fractal ‘F’ como la que satisface alguna(s) de las propiedades siguientes:
(1).- “F” posee detalle a todas las escalas de observación;
(2).- No es posible describir “F” con Geometría Euclidiana, tanto local
como globalmente;
(3).- “F” posee alguna clase de autosemejanza, posiblemente estadística;
(4).- La dimensión fractal de “F” es mayor que su dimensión topológica;
(5).- El algoritmo que sirve para describir “F” es muy simple, y
posiblemente de carácter recursivo.

En resumen, una técnica análoga a la que los biólogos aplican al concepto de vida.

Cuando observamos un fractal, de hecho, apreciamos algo que nos es familiar, más cercano que las perfectas figuras geométricas clásicas que nos han enseñado en el colegio.

Las ramificaciones de los árboles, las roturas imperfectas de una montaña o una costa, la disposición de la máxima superficie en un mínimo espacio de nuestro tejido pulmonar...

Los fractales nos acercan a la compleja "simplicidad" de la Naturaleza.

La estabilización del vacío cuántico y las dimensiones enrolladas

La dimensión fractal, tal como hemos visto en algunas anotaciones de esta bitácora, está formada por dos sumandos, la dimensión aparente o topológica más un factor dimensional tanto mayor cuanto más irregular es el fractal. Este factor aditivo en las fluctuaciones del incipiente Universo podría haber sido contrarrestado por las llamadas dimensiones enrolladas, que en cierta forma suponen una resta dimensional, en el momento en que nuestro Universo adoptó la configuración geométrica de tres dimensiones ordinarias y otras seis compactadas. El resultado pudo ser la propia existencia del cuanto de acción como factor de estabilidad de las fluctuaciones, pues su naturaleza las hace depender del inverso de la distancia permitiendo el vacío cuántico estable que conocemos. Resumiendo: Es posible que la configuración geométrica adoptada por nuestro Universo (tres dimensiones ordinarias y seis compactadas) haya sido determinante en la propia naturaleza del cuanto de acción y en la estabilidad del vacío cuántico. De esta cuestión trata el siguiente artículo publicado en la revista Ciencia Abierta (ISSN:0717-8948) de la Universidad de Chile, en el volumen 23, de marzo de 2004.


La existencia del cuanto de acción es la causa de que desaparezca el concepto clásico de trayectoria continua y deba ser sustituido por el de "trayectoria" fractal (discontinua, fracturada). El vacío absoluto y continuo de Newton, como marco estable de referencia, es sustituido por un vacío discontinuo y cambiante, merced a la propia estructura de la energía de sus fluctuaciones cuánticas. Nos encontramos, pues, ante un inmenso fractal, el propio vacío cuántico, modelado por sus fluctuaciones de energía de las que queremos extraer una información preciosa, que nos dará pistas sobre el propio Universo y su formación: su dimensión fractal.

El estudio de un fractal sencillo nos ayudará. En concreto, es interesante fijarnos en el que representa al llamado “movimiento browniano”, descubierto por Robert Brown, un botánico escocés que vivió entre finales del siglo XVIII y primera mitad del XIX. Estudió la flora de Australia y Nueva Zelanda y descubrió el llamado “movimiento browniano” de las partículas coloidales, que ha servido de base para el estudio de la cinética de los gases. Este movimiento browniano tiene mucho que ver con nuestro problema, su dimensión fractal es 2 , el típico de una variable puramente aleatoria que, en cierta forma, sobre un plano (dimensión topológica o aparente 2) sería capaz de recubrirlo.

Para variables con dimensión topológica distinta de la unidad es conveniente hablar del cociente D/ δ (dimensión fractal (D)/ dimensión topológica o aparente (δ) ) más que, simplemente, de su dimensión fractal. Reducimos así la dispersión de resultados y encontramos más fácilmente símiles con ejemplos sencillos como trayectorias unidimensionales. Dicho cociente para el fractal que representa al movimiento browniano será:

(1) D/ δ = ( δ + ε ) / δ = ( 1 +1 ) / 1 =2, donde el sumando positivo ε , que se añade a la dimensión topológica, es la dimensión del factor de arrugamiento y nos da una medida de su irregularidad, de su fractura y “arrugamiento”. En este caso ε = 1 .

La variable que representa el producto acotado:
(2) ( ∆ E ) ( ∆ x )< constante ( principio de incertidumbre, en donde ∆ t se ha sustituido por ∆ x / c ), es del mismo tipo que la relativa al movimiento browniano. El valor de este producto acotado es equivalente al paso que dan las partículas coloidales antes de chocar, puede tener cualquier valor aleatorio aunque acotado, por lo que su cociente D/δ es igualmente 2. Intuitivamente, este valor 2 nos indica que se deben dar n² pasos para poder alejarse de un punto arbitrario tan sólo n pasos efectivos.

En cierta forma, la dimensión fractal nos da una idea de magnitud encubierta, de compactación. Una trayectoria de dimensión fractal 3 es mucho más intrincada, más compacta que otra de dimensión fractal 2. Si hubiéramos seguido la trayectoria con un hilo ideal muy fino, en el primer caso el diámetro del ovillo resultante sería del orden de la raíz cúbica de la longitud total del hilo utilizado, en el segundo del orden de su raíz cuadrada. Observamos que existe una íntima relación entre la magnitud del ovillo, es decir su dependencia con la distancia, y su dimensión fractal. Cualquier fenómeno que modifique su dependencia con la distancia incidirá directamente en su dimensión fractal y viceversa.

Para nuestro caso, la energía de las fluctuaciones del vacío (la magnitud del “ovillo”) depende del inverso de la distancia, lo que supone un cociente D/δ igual a -1, que resulta completamente irregular e induce a pensar en la existencia de un factor desconocido que está influyendo en el cálculo e introduciendo una distorsión considerable.

El factor negativo, que supone una resta de dimensiones, me hizo pensar en las dimensiones enrolladas previstas por la teoría de supercuerdas, la más prometedora teoría que trata de unificar las cuatro interacciones fundamentales: gravedad, electromagnetismo, fuerza débil y fuerte. Dicha teoría necesita de 9 dimensiones espaciales para ser consistente, y ,dado que sólo conocemos 3, se ha especulado con la existencia de otras 6 que, supuestamente, estarían “enrolladas” sobre si mismas ,compactadas alrededor de un radio extremadamente pequeño (del orden de la longitud de Planck,10^-35 metros). Así para distancias mucho mayores que ese radio sólo serían perceptibles las 3 dimensiones ordinarias.

En cierta forma, para esas distancias, el número de dimensiones enrolladas se resta al total de las topológicas para dejar tan sólo 3 dimensiones aparentes. Una operación contraria al efecto de la dimensión del factor de arrugamiento, que se suma a la dimensión topológica.
En la expresión (1) si hallamos el cociente D/δ para un Universo con el mismo número de dimensiones enrolladas que la dimensión del factor de arrugamiento (transformación : δ −> δ − ε) , encontramos:

(3) D/δ = (δ ) / (δ - ε). Para ε = 6 , δ =3, el cociente D/δ toma el valor -1 de forma natural y lógica. Sin dimensiones enrolladas el factor ε = 6 supone una dimensión fractal 9 y una dependencia de la energía de las fluctuaciones con la raíz cúbica de la distancia (D/δ = 3) . El efecto de las dimensiones enrolladas la corrige hasta dejarla dependiente del inverso de la distancia, lo que repercute en la forma en que advertimos el vacío cuántico: completamente vacío y estable.
Para un universo con un número de dimensiones enrolladas (coeficiente dimensional negativo) igual a la dimensión del factor de arrugamiento (coeficiente positivo) de la energía de las fluctuaciones , se consigue la estabilización de esta energía que de otra forma dependería de la raíz cúbica de la distancia y no de su inverso. El vacío y toda la materia que contiene estarían deformados y serían inestables .

La especial geometría formada por las dimensiones ordinarias, las enrolladas y el tiempo permite un vacío cuántico estable que de otra forma haría imposible el Universo tal como lo conocemos, pues la turbulencia creada a todos los niveles impediría cualquier tipo de coherencia. Conforme nos acercamos a las distancias del orden de la longitud de Planck, este efecto estabilizador desaparece y se nos presenta un vacío deformado e inestable.

La transparencia del vacío, tal como la advertimos, puede que sea la mejor prueba de la existencia de las 6 dimensiones enrolladas.
También se puede leer un esbozo de la teoría en la revista Elementos de la Universidad de Puebla.