The Vacuum Energy Fractal, the Amazing Quantum Vacuum
En este post nos valemos de matemáticas elementales y un nuevo planteamiento para estudiar las propiedades de la energía del vacío como un simple fractal. Descubrimos las posibles dimensiones compactadas de la teoría de cuerdas y su importancia en la propia naturaleza del cuanto de acción (en muchas entradas de este blog, podeís leerlo en español, y en la referencia final de la Universidad de Puebla, México, o en Mi_ciencia_abierta).
Abstract
In this letter, we use elementary mathematics and a novel approach to study the properties of vacuum energy as a simple fractal. By applying fractal geometry, we can identify the compact dimensions and gain a better understanding of their significance in the fundamental nature of quantum action.
Keywords: Vacuum energy, compacted dimensions, relative fractal dimension, transition of dimensions, hypothetical quantum generalization
1 Introduction
The existence of Planck's quantum of action transforms Newton's classical and deterministic universe into a quantum universe, governed by Heisenberg's uncertainty principle. The vacuum contains a zero-point energy (ZPE) with a higher value as the distance considered becomes smaller. The minimum length, known as Planck's length (lp), is associated with a maximum energy called Planck's energy (Ep). For a distance n(lp), the associated energy is (Ep)/n, where "n" is a natural number. This property, conserved across all known scales, will assist us in analyzing this fractal. We will see that the relationship between ordinary dimensions and compact dimensions may have played an essential role in Planck’s quantum of action.
Fractal dimension is composed of two components: the topological dimension and a dimensional coefficient (topol_dim + dimens_coef). The more irregular the fractal, the higher the dimensional coefficient. For the purposes of our study, it is particularly interesting to examine simple fractals that possess a topological dimension of 1, such as the fractal path of Brownian motion.
Brownian motion (also known as Brownian movement) refers to various physical phenomena characterized by small, random fluctuations in some quantity. It was named after the Scottish botanist Robert Brown, who first studied these fluctuations in 1827 (britannica.com, December 23, 2021).
To move N effective steps in a straight line along one dimension, a particle moving with Brownian motion must take N2 total steps across two or more dimensions. The fractal dimension, a basic property of fractal lines [1], can be calculated using the relation log(N2) / log(N) = 2. In this case, the topological dimension is 1 and the dimensional coefficient is also 1. The value of 2 for the fractal dimension indicates that a linear movement, of topological dimension 1, can fill a plane of topological dimension 2.
In Brownian motion, and in general, fractal value = N2 = distancefractal_dimension.
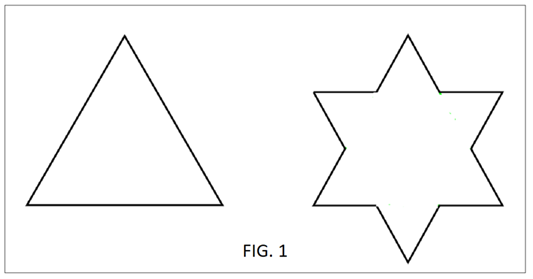
This can also be observed in the Koch curve, as shown in Figure 1. In the first iteration, the side that measures 3 segments becomes 4 segments. The fractal dimension is calculated as log 4 / log 3 = 1.26186. In one dimension, 3 segments become 4 segments in two dimensions (the plane):4= 31,26186, 4=3fractal_dimension (Mandelbrot, 1987).
3 Fractal dimension of vacuum energy
We know the dependence of vacuum energy on distance:
En = Ep / n = (Ep) (distance)-1.
If we live in hyperspace (according to string theory), we know the dependence of vacuum energy on distance in that space. Let En(hyper) be the value of the energy in hyperspace. Then:
log (En(hyper)) / log (En) = -1
This implies that vacuum energy is proportional to distance in hyperspace. Although energy has no topological dimension of 1, the quotient of the two logarithms behaves similarly to the case of Brownian motion. When comparing two energies, the topological dimension no longer matters because the result is a relative fractal dimension:
Relative fractal dimension = (topol_dim. + dimens_coef.)/(topol_dim.). To simplify we will write:
Relat_fr_dim. = (δ+ε)/δ (1).
So, we have: Relat_fr_dim= Log (En(hyper)) / log (En)= -1 = (δ+ε)/δ.
The -1 value reminds us of the compacted dimensions of the string theory, since while a positive dimensional coefficient indicates that the fractal occupies a space greater than its topological dimension, a negative dimensional coefficient indicates dimension compaction (Ruiz-Fargueta, 2004). The situation indicates a transition of dimensions such that:
T: δ àδ−ε.
The expression (1), with this
transition becomes: δ/(δ−ε) (2).
If the dimensional
coefficient is the same as the number of compact dimensions.
Expression (2) is consistent
with the value -1, since for d = 3 it gives us the value -6 for the number of
compact dimensions, which coincides with the value predicted by string theory.
Applying these values to the expression (1):
(δ+ε) / δ = (3+6)/3= 3 .
3 is the relative fractal dimension of the
vacuum energy, 9 its true fractal dimension.
The same result is found in
the following equivalent transformations:
T11
T12
The T11 transformation gives us the apparent result -1. But
the transformation T12 gives us the true result 3.
.
4 Generalization and possible transition of dimensions
The value -1 is the result of
En, as a function of distance, in the expression
(En)(n) <Constant, where
we have replaced the time (energy-time uncertainty principle) by the space (n)
traveled by the light in that time. If in this expression we add a fictitious
coefficient f, we will have:
(En) (nf) <Constant (3) (Hypothetical quantum generalization)
Now the transformations T11 and T12 will be:
T11: 1/nf à n }
T12: n à n2+f }
The true generalized result of the relative fractal dimension is
log(n2+f)/log(n) = 2+f, with the
expression (1): (δ+ε)/δ = 2+f (4)
During the transition of dimensions, the value of the fictitious coefficient f, associated with the very nature of the quantum (hypothetically), was defined. We will analyze the transition of dimensions combining expressions (3) and (4), for ε=9−δ:
(En)(n(ε−δ)/δ) <Constant.
Multiplying and dividing by nδ which is the generalized volume to ordinary dimensions δ:
(Energy_density) (nφ)<Constant. The value of φ = (δ2−2δ+9)/δ and is represented in figure 2.
For δ = 3 there is a minimum that corresponds to a maximum in energy density. For δ = 0, the value is infinite and corresponds to a minimum density equal to zero. The transition of dimensions from δ = 0, ordinary dimensions, to δ = 3, ordinary dimensions, takes us from a vacuum energy equal to zero to a maximum value. “In particular, our laws of physics arise from the geometry of the extra dimensions. Understanding this geometry ties string theory to some of the most interesting questions in modern mathematics, and has shed new light on them, such as mirror symmetry” (Polchinski, 2015)
5
Conclusion
It is possible that there was a transition of
dimensions that maximized the energy density of the vacuum for δ=3 (ordinary
dimensions) and ε=6 (compact dimensions). The nature of the quantum of action
may be tied to these specific values of δ and ε.
References
Mandelbrot, B. (1987), Los objetos fractales, Barcelona, Tusquets Editores.
Polchinski, J. (2015), String theory to the rescue. ArXiv: 1512.02477 v5 [hep-th]
Ruiz-Fargueta, J.S. (2004) El sorprendente vacío cuántico. Revista Elementos Universidad de Puebla BUAP.MX, 53, pp.52-53. (16/01/2022)https://elementos.buap.mx/directus/storage/uploads/00000002608.pdf







No hay comentarios:
Publicar un comentario