Impredecibilidad en la mecánica clásica
Independientemente de la precisión con que conozcamos el estado inicial de un sistema clásico (no cuántico) las imprecisiones tienden a crecer, de forma natural, con el tiempo y nuestra información inicial puede llegar a ser inútil para predecir su evolución futura. La mecánica clásica no es tan predecible como podría parecer a primera vista, tal como veremos en este post. Esta impredecibilidad se advierte claramente en el llamado problema de los tres cuerpos y se acentúa de forma dramática en los sistemas muy sensibles a las condiciones iniciales (caóticos).
El esquema de la mecánica newtoniana ha dado lugar a un impresionante cuerpo de ideas matemáticas conocido como mecánica clásica, de hecho, los nombres de muchos de los grandes matemáticos de los siglos XVIII y XIX están asociados a este desarrollo. Lo que se conoce como "teoría hamiltoniana", debida al matemático irlandés William Rowan Hamilton (1805-1865), resume gran parte de esa obra y, curiosamente, su formulismo fue muy importante para el desarrollo posterior de la mecánica cuántica. En el esquema hamiltoniano las posiciones y los momentos (producto de la velocidad por la masa) de cada partícula se tratan como si fueran variables independientes. De esta forma se obtienen dos conjuntos de ecuaciones, uno nos dice cómo cambian con el tiempo los momentos de todas las partículas (segunda ley del movimiento de Newton: fuerza = ritmo de cambio del momento), y el otro nos dice cómo cambian con el tiempo las posiciones. Y todas estas ecuaciones se derivan simplemente de una cantidad importante llamada función hamiltoniana H, que es la expresión para la energía total del sistema en términos de todas las variables de posición y momento.
Las ecuaciones hamiltonianas permiten visualizar de un modo muy potente y general la evolución de un sistema físico en un espacio abstracto llamado espacio de fases. Este espacio tiene para n partículas 6n dimensiones, tres coordenadas de posición y tres coordenadas de momento por cada partícula, y un simple punto representa el estado global del sistema físico, incluyendo los movimientos instantáneos de cada una de sus partículas.Las ecuaciones nos están diciendo cómo debe moverse este punto, cómo evoluciona el sistema en cada momento, y nos informan sobre su estabilidad. Esta estabilidad está íntimamente ligada a la posible dispersión de los puntos inicialmente próximos, es decir, si el sistema permanece localizado en cierta región R, a medida que pasa el tiempo, entonces estos puntos seguirán proximos y las imprecisiones en su especificación no se amplificarán con el tiempo. Por el contrario, cualquier dispersión indebida implicará una "impredecibilidad efectiva" en el comportamiento del sistema.
Sobre la dispersión de los sistemas hamiltonianos, y por tanto sobre la capacidad para predecir su comportamiento, existe un hermoso teorema debido al matemático francés Joseph Liouville (1809-1882) que nos dice que el volumen de cualquier región del espacio de fases debe permanecer constante en cualquier evolución hamiltoniana. Sin embargo, normalmente este volumen se dispersa debido a la extrema complejidad de su evolución (como los hilos del humo de un cigarro en una habitación). Aunque la región mantiene su volumen, se distorsiona y se estira hasta grandes distancias en el espacio de fases, y además el problema es mucho más grave en alta dimensión que en baja dimensión, porque hay muchas más direcciones en las que dipersarse.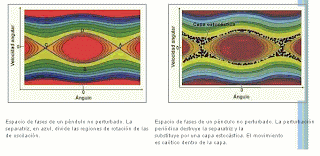
El teorema de Liouville nos sitúa ante un problema fundamental, pues de no existir todavía podríamos pensar que la tendencia de una región a extenderse por el espacio de fases podría quedar compensada por una reducción de volumen global, pero el teorema nos dice que eso es imposible, siendo ésta una característica universal de todos los sistemas dinámicos clásicos. Llegando más lejos con esta característica universal, nos hemos dado cuenta de que, precisamente, por esta tendencia a la difusión en el espacio de fases y a la dificultad que esto supone para mantener la organización de un sólido formada por millones de partículas, la mecánica clásica necesita de la mecánica cuántica para poder comprender, adecuadamente, la estructura real de los sólidos. Algo semejante al equilibrio que se mantiene en un átomo entre los electrones y el núcleo. Sólo la mecánica cuántica es capaz de explicarlo, para la mecánica clásica el resultado sería catastrófico pues sus leyes impedirían el equilibrio.
Los efectos cuánticos pueden impedir esta difusión en el espacio de fases. Paradójicamente, la solidez de un objeto que está compuesto de muchas partículas necesita de este efecto cohesionador de la mecánica cuántica. Si la mecánica clásica ha tenido tanto éxito en las predicciones sobre los cuerpos celestes es porque, para todos los cálculos, son considerados como puntuales y, por tanto, la dispersión de sus partes en el espacio de fases es practicamente despreciable.












No hay comentarios:
Publicar un comentario